Мысал. Пирсон критериін пайдаланып, 0,05 маңыздылық деңгейі кезіндегі таңдаманың эмпирикалық үлестірімімен бас жиынтықтың қалыпты үлестіруі жөнінде болжамның сәйкестігін тексеріңіз.
Шешуі:  және
және  табу үшін көбейту әдісін қолданамыз. Ол үшін 1-ші есептеуші
табу үшін көбейту әдісін қолданамыз. Ол үшін 1-ші есептеуші
кестені құрамыз.
| xi
| ni
| ui
| ni ∙ui
| ni ∙ui2
| ni ∙(ui+1)2
|
| -35
|
| -4
| -16
|
|
|
| -25
|
| -3
| -15
|
|
|
| -15
|
| -2
| -22
|
|
|
| -5
|
| -1
| -24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Σ
|
|
|
|
|
|
1 кесте
Жалған нөл С=5 болады (ең үлкен жиілігі бар варианта).
Һ=15-5=10 – қадам (екі көрші варианталардың айырмасы)
 - вариациялық қатардың көлемі.
- вариациялық қатардың көлемі.
Бақылау:  ; онда: 895=581+2∙77+160=895.
; онда: 895=581+2∙77+160=895.
Енді таңдамаларды есептейміз: орта мәнін ( ), дисперсияны
), дисперсияны  және орташа квадраттық ауытқуны (
және орташа квадраттық ауытқуны ( ).
).
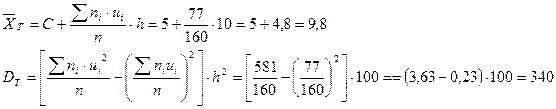
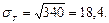
2) 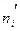 - теоретикалық жиіліктерді есептейміз, ол үшін 2-ші есептеуші кестені құрамыз, онда:
- теоретикалық жиіліктерді есептейміз, ол үшін 2-ші есептеуші кестені құрамыз, онда:
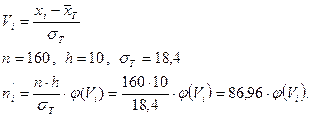
 - Лаплас функциясы (оның мәндері бірінші қосымшадан алынады).
- Лаплас функциясы (оның мәндері бірінші қосымшадан алынады).
 - жұп функция.
- жұп функция.

| 
| 
| 
| 
| 
|
|
| -35
| -44,8
| -2,43
| 0,0208
|
|
|
| -25
| -34,8
| -1,89
| 0,0669
|
|
|
| -15
| -24,8
| -1,35
| 0,1604
|
|
|
| -5
| -14,8
| -0,8
| 0,2897
|
|
|
|
| -4,8
| -0,26
| 0,3857
|
|
|
|
| 5,2
| 0,28
| 0,3836
|
|
|
|
| 15,2
| 0,83
| 0,2827
|
|
|
|
| 25,2
| 1,37
| 0,1561
|
|
|
|
| 35,2
| 1,91
| 0,0644
|
|
|
|
| 45,2
| 2,46
| 0,0194
|
|
2 кесте
 критериінің бақылау мәнін табу үшін 3 – ші кестені құрамыз:
критериінің бақылау мәнін табу үшін 3 – ші кестені құрамыз:

| 
| 
| 
| 
| 
|
|
|
|
|
|
|
|
|
|
|
| -1
|
| 0,167
|
|
|
|
| -3
|
| 0,643
|
|
|
|
| -1
|
| 0,04
|
|
|
|
|
|
| 0,735
|
|
|
|
| -2
|
| 0,121
|
|
|
|
|
|
| 0,36
|
|
|
|
| -5
|
| 1,786
|
|
|
|
| -1
|
| 0,167
|
|
|
|
|
|
|
|

|
|
|
|
|  
|
3 кесте
Сонымен,  - формуладан табамыз, сонда
- формуладан табамыз, сонда  болады. К=S-3 еркіндік дәреже санын есептейміз, мұнда S-таңдаманың топтар саны (варианталар саны). Енді
болады. К=S-3 еркіндік дәреже санын есептейміз, мұнда S-таңдаманың топтар саны (варианталар саны). Енді  2 (хи – квадрат) үлестірімнің кризистік нүктерлер қосымшадан
2 (хи – квадрат) үлестірімнің кризистік нүктерлер қосымшадан  2
2  мәнін табамыз. Ол тең болады -
мәнін табамыз. Ол тең болады -  .
.  мен
мен 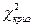 салыстырамыз, бізде
салыстырамыз, бізде  <
< 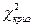 (8,019<14,1), сондықтан
(8,019<14,1), сондықтан  болжамы қабылданады, яғни эмпирикалық және теоретикалық жиілік айырмалары маңызды емес. Демек, Пирсон критериінің мәні қабылдау облысында жатыр дейміз.
болжамы қабылданады, яғни эмпирикалық және теоретикалық жиілік айырмалары маңызды емес. Демек, Пирсон критериінің мәні қабылдау облысында жатыр дейміз.

 және
және  табу үшін көбейту әдісін қолданамыз. Ол үшін 1-ші есептеуші
табу үшін көбейту әдісін қолданамыз. Ол үшін 1-ші есептеуші - вариациялық қатардың көлемі.
- вариациялық қатардың көлемі. ; онда: 895=581+2∙77+160=895.
; онда: 895=581+2∙77+160=895. және орташа квадраттық ауытқуны (
және орташа квадраттық ауытқуны (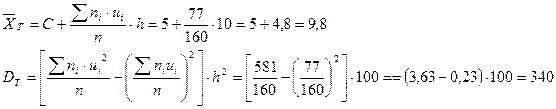
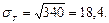
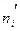 - теоретикалық жиіліктерді есептейміз, ол үшін 2-ші есептеуші кестені құрамыз, онда:
- теоретикалық жиіліктерді есептейміз, ол үшін 2-ші есептеуші кестені құрамыз, онда: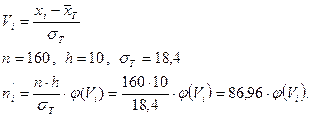
 - Лаплас функциясы (оның мәндері бірінші қосымшадан алынады).
- Лаплас функциясы (оның мәндері бірінші қосымшадан алынады).





 критериінің бақылау мәнін табу үшін 3 – ші кестені құрамыз:
критериінің бақылау мәнін табу үшін 3 – ші кестені құрамыз:







 - формуладан табамыз, сонда
- формуладан табамыз, сонда  болады. К=S-3 еркіндік дәреже санын есептейміз, мұнда S-таңдаманың топтар саны (варианталар саны). Енді
болады. К=S-3 еркіндік дәреже санын есептейміз, мұнда S-таңдаманың топтар саны (варианталар саны). Енді  2 (хи – квадрат) үлестірімнің кризистік нүктерлер қосымшадан
2 (хи – квадрат) үлестірімнің кризистік нүктерлер қосымшадан  мәнін табамыз. Ол тең болады -
мәнін табамыз. Ол тең болады -  .
.  мен
мен 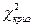 салыстырамыз, бізде
салыстырамыз, бізде  болжамы қабылданады, яғни эмпирикалық және теоретикалық жиілік айырмалары маңызды емес. Демек, Пирсон критериінің мәні қабылдау облысында жатыр дейміз.
болжамы қабылданады, яғни эмпирикалық және теоретикалық жиілік айырмалары маңызды емес. Демек, Пирсон критериінің мәні қабылдау облысында жатыр дейміз.


