Группа. Моделирование полета тела, брошенного под углом к горизонту
Постановка задачи В процессе тренировок теннисистов используются автоматы по бросанию мячика в мишень. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенной высоты, находящуюся на известном расстоянии. Основные предположения: – мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой; – изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с, и движение по оси Y можно считать равноускоренным; – скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь, и движение по оси X можно считать равномерным. Пусть мишень высотой h будет размещаться на расстоянии s. Если, l – высота мячика над землей на расстоянии s. То попадание произойдет, если значение высоты l мячика будет удовлетворять условию 0 ≤ l ≤h. Исходными данными для данной модели являются: начальная скорость V0, угол бросания α, высота мишени h, расстояние, на котором расположена мишень s. Результат – значение высоты l мячика. В зависимости от величины l, выдается сообщение «недолет», «перелет» или «попадание». Математическая модель Для формализации модели используются известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости V x = y = Пусть мишень высотой h будет размещаться на расстоянии s. Из формулы (1) выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s: t = s/ Подставляем это значение для t в формулу (2). Получаем l – высоту мячика над землей на расстоянии s: L:= S*tgα – g* Попадание произойдет, если значение высоты l мячика будет удовлетворять условию: 0 ≤ l ≤h. Если l < 0, то это означает «недолет», а если l > h, то это означает «перелет». Вычислительный эксперимент Выполнить моделирование полета тела, брошенного под углом к горизонту. Предусмотреть: – ввод исходных данных: начальной скорости V0, угла бросания α, высоты мишени h, расстояния, на котором расположена мишень s; – расчет значения высоты l мячика; – в зависимости от величины l выдача сообщения «недолет», перелет» или «попадание»; – построение траектории движения мячика.
|

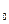 и угле бросания α, значения координат дальности полета x и высоты y от времени можно описать следующими формулами:
и угле бросания α, значения координат дальности полета x и высоты y от времени можно описать следующими формулами: *cosα*t; (1)
*cosα*t; (1) /2 (2)
/2 (2) /2*
/2*  *cos2α (4)
*cos2α (4)


