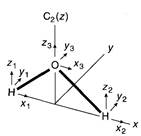
Представления для движений атомов Н и О

На рис 5.4 (a) представлены векторы х₁ и х₂ двух атомов водорода. Как мы ранее видели

Рис. 5.4

, молекула Н₂О имеет симметрию С_2v и для того, чтобы получить представления, используя эти векторы в качестве базиса, мы примем к рассмотрению характеры матриц, которые описывают влияние различных операций симметрии (Е, С₂ и т.д.) на данную пару векторов, помня при этом, что только те векторы, которые остаются несмещёнными будут вносить свой вклад в характер.

Каждая из операций Е и σ_v (xz) оставляют эти векторы несдвинутыми, что приводит к матрице с харатером +2, в то время как для операций С₂ и σ_v' (yz) результирующий характер равен нулю.

Приводимое представление поэтому выглядит таким образом:

С2v	E	C2	sv(xz)	s¢v(yz)
ГH(x)

 

Сверившись с таблицей характеров для группы С_2v, получим, что это выражение может быть упрощено до А₁ + В₁.

Подобным образом на рис 5.4 (b) и (c) показаны y и z векторы соответственно для двух атомов водорода, и представления, возникающие отсюда:

С2v	E	C2	sv(xz)	s¢v(yz)
ГH(y)			-2		=	A2+B2

 

И

 

ГH(z y)

-2

=

A1+B1

 

Неприводимое представления для движений атомов водорода поэтому следующее:

Г_{H ( xyz )} = 2А₁ + А₂ + 2В₁ + В₂

На рис 5.5 представлены векторы x, y и z для атома кислорода. Через этот атом

Рис. 5.5

проходят все элементы симметрии, но некоторые операции приводят к изменению направления вектора на противоположное (внося вклад -1 в характер), в то время как остальные оставляют и положение и направление векторов без изменений. Представление для движений атома кислорода становится следующей:

С2v	E	C2	sv(xz)	s¢v(yz)
ГO(x yz)		-1			=	A1+B1+B2

 

с результатом, идентичным ранее полученному для атома, находящегося в исходной точке системы координат (см. Часть 3, Рис. 3.3).

Общее представление для движений атомов в молекуле Н₂О получается объединением вкладов каждого из двух типов атомов, и поэтому равно:

Г_mol = Г_Н + Г_О = 3А₁ + А₂ + 3В₁ + 2В₂

5.4 Г_mol из первых- значение несмещённых атомов.

Вывод (получение) Г_mol непосредственно путём расчета влияния операций симметрии на все векторы атомов одновременно на первый взгляд кажется удручающей перспективой - даже для трехтомных молекул, таких как Н₂О. Для этого требуется выведение (расчет, получение) четырёх матриц 9´9, которые описывают влияние (эффект), производимый четырьмя операциями симметрии точечной группы С_2v на девять векторов х₁, у₁, z₁, x₂, y₂, z₂ и т.д., показанных на Рис. 5.6.

Самая простая из этих матриц возникает при описании эффекта операции идентичности

Рис. 5.6

. Данная операция оставляет все векторы без изменений и приводит к матрице 9´9 с характером 9 (Рис. 5.7)

Операция С₂ (рис 5.8), наоборот, оставляет неизменённым только один вектор (z₃), меняет на противоположные знаки х₃ и у₃, но сдвигает все векторы атомов Н, т.е. C₂ (z₁) ® (z₂)

Рис. 5.7

 

Рис. 5.8

 

Это приводит к возникновению (появлению, постановке) нолей на диагоналях для данной и других операций, которые подобным образом перемещают вектор, и источником этого является то, что атомы водорода сами меняются позициями в результате операции С ₂.

Поэтому только три вектора: х₃, у₃ и z₃ вносят вклад в характер с результирующим эффектом -1.

Положение относительно отражений в σ_v' (yz) такое же. Так, атомы водорода снова меняются позициями, в результате чего их векторы не вносят вклада в характер. Только атом О остаётся несмещённым и вклад в характер от х₃, у₃ и z₃ теперь -1, +1 и +1, что приводит к общему значению характера +1.

Отражение в плоскости молекулы, σ_v (xz), оставляет все атомы несмещёнными, но меняет на противоположные знаки векторов у, в то время как x и z остаются без изменений. Каждый несмещённый атом таким образом вносит вклад +1 в характер, и, поскольку фактически при этой операции три атома остаются несмещёнными, общий вклад в характер равен +3.

Мы можем видеть, что характеры приводимого представления, полученного данным путём, такие:

С2v	E	C2	sv(xz)	s¢v(yz)
Гmol		-1

 

Используя формулу приведения мы можем упростить данное представление до:

Г_mol = 3А₁ + А₂ + 3В₁ + 2В₂

результата, идентичного полученному ранее.

Основные выводы, к которым ми пришли таким образом:

1. Только векторы несмещающихся атомов могут вносить вклад в характер приводимого представления.

2. Величина этого вклада зависит от типа элемента симметрии (Е, С₂ и т.д.)

 

5.5 Трансляционная, вращательная и колебательная симметрия в молекуле Н ₂ О

Результат, полученные нами ранее, различает в молекуле Н₂О девять степеней свободы на основе (выраженный) их симметрии, и первым шагом при определении симметрии колебаний является понимание (признание) того, что общее представление, складывается (состоит) из независимых (отдельных) представлений для трансляции, вращения и колебания. Это может быть записано как

Г_mol = Г_trans + Г_rot + Г_vib

И если главной нашей задачей является обнаружение симметрии молекулярных колебаний, то, очевидно, что

Г_vib = Г_mol - Г_trans - Г_rot

Как мы уже знаем, Г_mol = 3А₁ + А₂ + 3В₁ + 2В₂, и всё, необходимо для того, чтобы выяснить, какие из этих представлений описывают симметрию колебаний, это выявить неприводимые представления, которые составляют Г_trans и Г_rot.Эту информацию можно легко получить из таблицы характеров для точечной группы С_2v:

С2v	E	C2(z)	sv(xz)	s¢v(yz)	h =4
А1					z	x2, y2, z2
А2			-1	-1	Rz	xy
В1		-1		-1	x, Ry	xz
В2		-1	-1		y, Rx	yz

 

Молекула воды нелинейна, и поэтому представление Г_rot имеет три составляющих: R _x, R _y и R _z, соответствующих вращению вокруг каждой из координатных осей. Симметрия R _x, R _y и R _z приведена в предпоследнем столбце таблицы характеров группы С_2v, где мы можем увидеть, что они принадлежат представлениям В₂, В₁ и А₂ соответственно. Вращательные степени свободы равны:

Г_rot = А₂ + В₁ + В₂

Представления, которые вносят вклад в Г _trans, также могут быть получены из таблицы характеров. В данном случае это функции х, у и z которые направлены (относятся) к представлениям для поступательного движения (трансляционных движений). Эти функции также представлены в предпоследнем столбце таблицы характеров. Таким образом, для точечной группы С_2v:

Г _trans = А₁+В₁ + В₂

В некоторых изданиях функции обозначены как Т _x, Т _y и Т _z что подтверждает это описание.

Теперь мы в состоянии вывести симметрию колебательных мод в молекуле Н₂О:

Г_vib = Г_mol - Г_trans - Г_rot = (3А₁ + А₂ + 3В₁ + 2В₂) - (А₂ + В₁ + В₂) - (А₁+В₁ + В₂)

т.е.

Г_vib = 2А1 +В1

 

5.6 Графическое изображение трансляций, вращений и колебаний в молекуле Н₂О.

Математические выражения, которые мы получили ранее для симметрии различных степеней свободы в молекуле Н₂О, изначально дают нам небольшое представление о типах сложных (запутанных) атомных движений. Часто полезно обратиться к смещению исходных декартовых векторов для того, чтобы сделать происходящее более наглядным. Также это проиллюстрирует существенные особенности колебаний типа А₁ и В₁. Поступательная степень свободы представлена движением всей молекулы вдоль трёх

Рис. 5.9

координатных осей, как показано на рис 5.9, и точно также легко представить наглядно вращения R _x и R _z (рис 5.10). Однако, оставшаяся степень свободы, R _y, и три колебания требуют дальнейшего исследования.

Симметрии этих представлений – В₁ (R _y) и 2А₁ + В₁ (колебания) и дело обстоит так, что движения атомов в этих степенях свободы происходят в плоскости (xz) молекулы. На рис 5.11 (а) и (b) показаны два набора смещений векторов, которые имеют симметрию В₁ и которые почти, но не полностью соответствуют вращательным и колебательным движениям соответственно.

Рис. 5.10

 

Если мы посмотрим сначала на рис 5.11 (а), становится очевидно, что хотя движение является преимущественно вращательным относительно оси y, перемещения в указанном направлении будут изменять длины связей, а также смещать центр масс молекулы. Поэтому такое движение не является вращением в чистом виде. Подобным образом, смещения атомов на рис 5.11 (b) приводят главным образом к изменениям в длинах связей, но при этом присутствует и небольшое вращение.

Рис. 5.11

 

Ни один из этих рисунков в точности не соответствует колебанию или вращению, и фактические перемещения (смещение, сдвиги), которые имеют место в этих двух степенях свободы, в большей степени похожи на векторы, показанные на соответствующих диаграммах 5.11 (c) и (d). Тем не менее, все четыре рисунка показывают основные особенности симметрии типа В₁, которая является основной асимметрией вдоль оси x.

На рис 5.12 (а) и (b) показаны идеализированные движения двух колебаний А₁, которые могут быть построены с помощью имеющихся Декартовых векторов. Вибрации, подобные этим и относящиеся к полностью симметричным представлениям, часто описывают как «полностью симметричные моды», и их характерной особенность в том, что на всех стадиях колебания молекула сохраняет все элементы симметрии, которые присутствуют в равновесной структуре.

Тем не менее, как мы ранее обнаружили для смещения типа В₁, хотя бы одно из изображённых на рис 5.12 (а) движений предположительно не может быть полностью колебательным, так как оно включает в себя и смещение центра масс. И снова представленные на рисунке диаграммы (с) и (d) предлагают нам более реалистичную картину реальных смещений атомов.

 

Рис. 5.12

К счастью, наше дальнейшее использование симметрии колебаний не зависит то знания точных смещений атомов, и, конечно, они рассчитываются только иногда. Всё, что нам нужно - это симметрия.

 

5.7 Вклад в характер от несмещённых атомов - другие операции симметрии

Большое значение для определения Г_mol для молекулы Н₂О был тот факт, что нужно было принимать в расчет только те атомы, которые не смещались при проведении операции симметрии для того, чтобы вычислить характеры соответствующих (связанных с ними) матриц. В частности, мы видели, что вклад от несмещённых атомов в матрицы для операций Е, С₂, σ_v (xz) и σ_v' (yz) равны + 3, -1, +1 и +1 соответственно.

Для того, чтобы быть полностью овладеть решением подобных проблем, мы должны рассмотреть вклад от других операций симметрии.

В части 4 мы видели, что эффект действия оси С_n на точку (X,Y,Z) вносит в характер матрицы, описывающей операцию С_n вклад, определяемый как:

χ С_n¹ = 2cos q +1

Это уравнение также определяет вклад, который вносит простое вращение в характер Г_mol для каждого несмещённого атома.

Таким образом для операции С₂, q =180^о, cos180^о = -1 и общий вклад в характер равен -1 для каждого несмещенного атома. Для С₄¹, cos q = 0 и вклад равен +1.

В этом уравнении слагаемое «2cos q» возникает в результате вращения в плоскости xy, а слагаемое «+1» возникает вследствие того факта, что когда ось С_n совпадает с осью z, операция С_n¹оставляет любой вектор, расположенный вдоль оси z без смещений.

Если вместо операции С_n¹ мы рассмотрим операцию поворота с отражением S_n¹, мы

Таблица 5.1Вклады в характеры от неподвижных атомов для обычных операций симметриии
Операция симметрии	Вклад в характер
E (=C1)
i (=S2)	-3
s (=S1)
C2	-1
C3
C4
C6
S3	-2
S4	-1
S6

наглядно убедимся, что вклад плоскости xy такой же, но компонент «отражения» для этой операции теперь приведёт к тому, что любой вектор, расположенный вдоль z, сменит своё направление на противоположное. Соответствующее уравнение для операции S_n¹ поэтому имеет вид:

χ S_n¹ = 2cos q -1

Теперь мы способны вывести вклад от несмещаемых атомов в Г_mol для всех С_n и S_n операций симметрии, и примеры таких расчетов приведены в таблице 5.1. Для полной картины в эту таблицу также включены компоненты, возникающие из идентичности (Е), из атома, лежащего в центре инверсии (i) и от атома, находящегося на любой плоскости (σ)