Симметрия валентных колебаний

Как показано ранее, симметрия валентных колебаний в молекуле может быть получена из представлений, выведенных из связей. Для молекул, которые содержат связи более чем одного типа, таких как SO₂F₂, валентные моды могут можно подразделить на два типа: валентные колебания S-O и колебания связи S-F.

Для того, чтобы продемонстрировать общую процедуру получения симметрии валентных мод, удобно для начала вернуться к рассмотрению двух молекул - Н₂О и SO₂F₂, для которых уже было получено полное колебательное представление Г_vib.

 

Валентные моды в Н₂О

Симметрия валентных мод в молекуле Н₂О получается упрощение (приведением)

Рис. 5.16

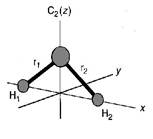
представления Г, которое относится к двум связям О-Н. Молекула воды имеет симметрию C_2v и если мы обозначим связи как r₁ и r₂ (Рис. 5.16), характер приводимого представления Г:

Что может быть потом упрощено до

Г_r = Г_stretch = А₁ + В₁

Этот результат, выведенный в главе 3 как простое упражнение, теперь приобретает большее значение. Данное неприводимое представление описывает симметрии двух валентных мод в молекуле Н₂О.

Ранее мы уже видели, что молекула воды имеет в целом три колебания 2А₁ + В₁, и приблизительные движения атомов при этих колебаниях воспроизведены на рис 5.17. Это независимый вывод симметрий валентных колебаний разрешает нам использовать зависимость:

Г_vib = Г_stretch + Г_bend = 2А₁ + В₁

 

Из которой следует, что Г_bend =А1.

Экспериментально для молекулы Н₂О были найдены колебательные моды при 3756, 3657

Рис. 5.17

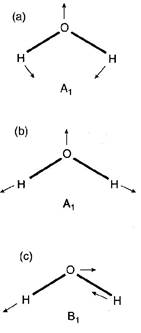
и 1595 см^-1. Таким образом, одно из колебаний наблюдалось при значительно более низкой частоте, чем два других, и было идентифицировано как деформационное колебание А₁, ((Рис. 5.17 (а)). Две более высокочастотных моды соответствуют двум валентным колебаниям, и может быть показано, что при 3657 см^-1 наблюдается то из колебаний, которое имеет симметрию А₁, включающее синхронное (одновременное) растяжение обеих связей (Рис. 5.17 (b)), в то время как мода 3756 см ^-1 имеет симметрию В₁. В этом случае одна связь удлиняется, в то время как вторая - укорачивается (Рис. 5.17 (с)), и такой тип движений часто описывают как «асимметричное валентное колебание».

Эти результаты для молекулы воды также иллюстрируют два важных общих выводы (результата). Во-первых, хотя две связи О-Н в молекуле воды эквивалентны, симметричны (А₁) и антисимметричные (В₁) валентные колебания, для которых были найдены различные частоты колебаний, и в общем было установлено что каждая колебательная мода в молекуле имеет уникальную (особенную) частоту.

Во-вторых, использование двух связей r₁ и r₂ как базиса для приводимого представления валентных мод привело к возникновению двух неприводимых представлений, в данном случае А₁ + В₁. Это соответствие между количеством связей и числом связанных с ними неприводимых представлений также является достаточно общим результатом. При использовании этой зависимости, однако надо принимать во внимание любые вырождения, которые могут присутствовать (как мы увидим ниже), а термин «связь» будет интерпретирован просто как расстояние между ядрами без рассмотрения (включения) порядка связи. Так, связь С-С в С₂Н₄ будет рассматриваться как простое (единичное, одинарное) межъядерное расстояние, но не как отдельные σ и π связи. С такой оговоркой, количество валентных мод в молекуле соответствует количеству связей.

 

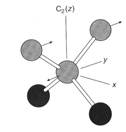
Валентные колебания в SO₂F₂

Молекула SO₂F₂ имеет симметрию C_2v и ранее было установлено, что представления для

Рис. 5.18

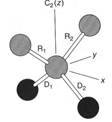
всех колебаний имеет вид:

Г_vib = 4А₁ + А₂ + 2В₁ + 2В₂

Имеющиеся в молекуле две связи S-O и две S-F связи могут быть обозначены как R₁, R₂, D₁ и D₂ как показано на рис 5.18.

Эти четыре связи дают начало четырём валентным модам, но. Поскольку присутствуют два различных типа связей, R и D, валентные моды могут быть подразделены на две группы, Г_R и Г_D.

Характеры приводимых представлений Г_R и Г_D получены обычным путём, с учётом того. как много связей из группы (набора) остаются несмещёнными при операциях симметрии в группе C_2v.

	E	C2	sv(xz)	s¢v(yz)
ГR
ГD

и соответствующие неприводимые представления либо проверкой

Рис. 5.19 (а) Симметричное S-O валентное колебание

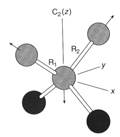
либо используя формулу приведения.

Г_R = А₁ + В₂, Г_D = А₁ + В₁

В составе общего представления Г_vib четыре валентных моды вносят 2А₁+В₁ +В₂. а оставшиеся представления соответствуют деформационным колебаниям:

Г_bend = 2А₁ + А₂ + В₁ + В₂

Экспериментальные данные дают четыре валентных колебания при 1502, 1269, 885 и 848

см^-1. Пара с более высокими частотами соответствует двум растяжениям связи S-O, другая пара – растяжениям связи S-F. В каждой из этих пар есть «симметричные растяжения» и «антисимметричне растяжения», и смещения атомов, связанные с валентными модами S-O показаны на рис 5.19 (а) и (b). На практике, как мы уже видели на примере молекулы Н₂О, эти векторы дают только приблизительную картину смещений атомов, но этого

Рис. 5.19 (b) Асимметричное S-O валентное колебание

достаточно для того, чтобы показать симметрии различных мод.

Третий важный общий вывод. Один из результатов, которые выявился из определения симметрий валентных мод в Н₂О и SO₂F₂ состоит в том, что каждый набор эквивалентных связей r, R или D приводит к появлению полносимметричного представления, в данном примере А₁,

поскольку обе молекулы относятся к точечной группе C_2v.

Это пример достаточно общего результата: всегда возможно растянуть набор эквивалентных связей так, чтобы полная симметрия молекулы сохранилась.

Исходя из этого, представление полученной из набора эквивалентных связей (r) всегда будет содержать полностью симметричное представление.