Примечание об обозначении орбиталей.

Представления, относящиеся к различным таблицам характеров, идентифицируются с помощью системы обозначений, которая содержит заглавные буквы (или греческие символы в случае линейных молекул). Тем не менее, при обозначении атомных орбиталей, к примеру, на диаграммах, общепринятым является использование строчных букв вместо заглавных.

Поэтому индивидуальные (отдельные) d –орбитали в D_4h окружении будут обозначаться как a_1g + b_1g + b_2g +e_g и s –орбитали как a_1g.

Из этого можно сделать два общих вывода:

1. s –орбитали центрального атома всегда преобразуются в соответствии с полностью симметричным представлением.

2. Другие орбитали центрального атома (т.е. p- или d-) преобразуются тем же образом, что и математические функции, которые возникают (проявляются) как их подписи (подстрочные индексы), обращая внимание на упрощение, которое делается в случае 2z ²- x ² - y ².

 

7.5 σ-связи в СН₄.

Теперь мы можем построить диаграмму молекулярных орбиталей для связывания в СН₄. Это

Рис. 7.7

делается путём комбинирования орбиталей центрального атома с орбиталями лигандов той же самой симметрии, и приводить к возникновению связывающих и антисвязывающих комбинаций. Валентные орбитали атома углерода (2 s и набор 2 p) в тетраэдрическом окружении преобразуются в a ₁ и t₂ соответственно. Набор из четырёх орбиталей атомов водорода преобразуется, соответственно в a ₁ + t₂, и на Рис. 7.7 показана диаграмма молекулярных орбиталей, описывающая эффект от комбинирования этих наборов атомных орбиталей. В метане в общем есть восемь валентных электронов, четыре - от атома углерода и по одному от четырех атомов водорода, и это как раз то количество кторое нужно, чтобы заполнить связывающие уровни a ₁ + t₂

 

7.6 Комбинации р_σ орбиталей: σ-связи в XeF₄

Приводившиеся ранее примеры показывают, каким образом набор s -орбиталей может

Рис. 7.8

взаимодействовать с центральным атомом, образуя σ-связь, но p -орбитали с их лопастями, лежащими вдоль межъядерных осей (линий, соединяющих ядра атомов?) также могут принимать участие в σ-связывании, так как в этой ориентации они аксиально симметричны (осесимметричны) (так как в таком расположении?).

На рис 7.8 показаны четыре p -орбитали атомов фтора в молекуле XeF₄(D_4h), которые лежат вдоль связей Xe-F. В такой пространственной ориентации ониведут себя как s -орбитали, и их представление Г _p в D_4h поэтому является идентичным выведенному ранее для валентных мод в XeF₄: Г =a_1g + b_1g + e_u

Центральный атом ксенона имеет орбитали matching (подходящей) симметрии 5 s (a_1g), 5 d_x2-y2 (b_1g) и пару 5 p_x, 5 p_y (e_u), и, как и описанном выше примере для СН₄, может быть построена диаграмма молекулярных орбиталей, в которой орбитали ксенона и фтора одной и той же симметрии взаимодействуют, образуя связывающие и антисвязывающие комбинации. На Рис. 7.9 показаны связывающие комбинации p - орбиталей ксенона и s -орбиталей фтора в системе σ -связей для XeF₄.

Рис. 7.8 σ-связывание в XeF4

 

 

7.7. Внеплоскостное связывание в XeF₄

 

На рис 7.10 показана ориентация p_z орбиталей четырёх атомов фтора в XeF₄, и очевидно что

Рис. 7.10 pz орбитали атомов фтора в XeF4

они не предполагают возможность внеплоскостного π-связывания для (что ксасется, по отношению) к одинарной Xe-F связи. Однако, для того, чтобы установить симметрию любых возможных молекулярных π -связей, мы должны получить неприводимое представление для Г_π в точечной группе D_4h.

Характеры для матриц, составляющих Г_π получены обычным образом, при рассмотрении эффекта, оказываемого различными операциями симметрии на четыре p_z орбитали, при этом помня, что орбитали фтора, находящиеся вне плоскости могут менять свой знак, (переворачиваться?) при таких операциях симметрии как σ_h. Используя разработанную (принятую) ранее (см. Рис. 1,12) ориентацию молекулы, получаем:

	E	2C4	C2	2C2¢	2C2¢¢	i	2S4	sh	2sv	2sd
Гπ				-2				-4

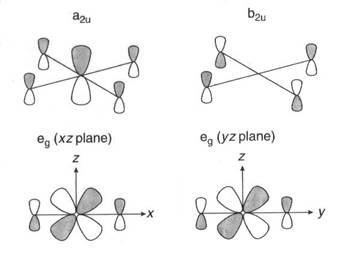
Что сводится к Г_π =a_2u + b_2u + e_g

Таблица характеров группы D_4h показывает, что для того, чтобы взаимодействовать с этими комбинациями p_z орбиталей атомов фтора, (правильную) подходящую симметрию имеют такие орбитали центрального атома ксенона: 5 p_z (a_2u) и пара орбиталей 5 d_xz и 5 d_yz, которые вместе преобразуются в e_g. У атома ксенона нет орбиталей с симметрией b_2u. На Рис. 7.11 показаны a_2u и e_g комбинации атомных орбиталей, которые приводят к net связыванию, а также несвязывающие b_2u комбинации орбиталей F.

Рис. 7.11 Внеплоскостное π-связывание в XeF4

 

 

7.8 σ- и π- орбитали лигандов в октаэдрических комплексах МХ₆

И, наконец, в этой главе мы рассмотрим возможности σ- и π-связывания в октаэдрических

Рис. 7.12

комплексах переходных металлов с точки зрения симметрии. Так же, к и в приведенных ранее примерах, π-орбитали лигандов опять обычно являются p -орбиталями, перпендикулярными σ-связи, но так как s - и p - орбитали центрального атома уже полностью вовлечены в σ-систему, мы можем ожидать, что любое π-связывание должно включать в себя d- орбитали металла.

Для начала нужно понять, что каждый лиганд Х в общем имеет одну доступную p -орбиталь σ-симметрии, которая направлена к центральному атому М и которая будет вовлечена в σ-связь, и две других p -орбитали, перпендикулярных к связи М-Х, которые доступны для π-связывания. Расположение этих p -орбиталей относительно связи М-Х показано на рис 7.12. В общем, существуют шесть лигандов, координированных к (связанных с) к металлу, и, следовательно, есть шесть р- орбиталей лигандов, которые могут принимать участие в σ-связывании, и 12 р- орбиталей лигандов в возможной π-системе.

Можно принять, что представление для σ-связывания лигандов, Г_σ идентично Г_stretch для МХ₆. Оно было выведено ранее как Г _stretch = А_1g + Е_g + T_1u (часть 6), и, применяя этот результат к σ -орбиталям, мы должны только помнить об обозначениях строчными буквами. Следовательно Г_σ = a_1g + e_g + t_1u. Центральный атом может предоставлять орбитали с такой симметрией и на Рис. 7.13 показаны σ-связывающие комбинации лигандов и орбиталей металла.

 

Рис. 7.13 Внеплоскостное π-связывание в XeF4

Представление Г_π можно получить, рассматривая эффект оказываемый различными операциями симметрии точечной группы О_h на 12 р -π орбиталей лигандов, и затем приводя получившееся представление с помощью формулы приведения. Эта процедура работает удовлетворительно, но есть ряд альтернативных и более быстрых методов, которые используют тот факт, что р -орбитали атомов преобразуются (трансформируются) таким же образом, как и смещения атомов x, y и z. Отсюда, для каждого лиганда Х

Г_p = Г_mol

Если мы определим Г_Х как представление для всех 18 р -орбиталей Х-лигандов, тогда

Г_Х = Г_σ + Г_π

Тем не менее, из-за эквивалентности р- орбиталей и x, y и z, Г_Х эквивалентно ранее рассчитанному Г_mol для набора из шести атомов лигандов Х.

Поэтому нам нужно только рассчитать Г_mol для шести атомов лигандов, а затем получим Г_π из равенства Г_π = Г_mol – Г_σ.

Зная число несмещённых атомов и вклад от несмещённого атома мы, используя описанный в части 5 способ, получим Г_mol в таком виде:

	Е	8С3	6С2¢	6С4	3С2 (=С24)	i	6S4	8S6	3σh	6σd
Кол-во неподвиж-ных атомов
Вклад от каждого атома (табл. 5.1)			-1		-1	-3	-1
Гmol					-2

 

Что может быть упрощено с помощью формулы приведения, приводя нас к выражению:

Г_mol = a_1g + e_g + t_1g + t_2g + 2t_1u + t_2u

Представление Г_σ выведено как a_1g+e_g+t_1u, и комбинация симметрии для 12 орбиталей лигандов, способных участвовать в π-связывании поэтому выглядит как:

Г_π = t_1g + t_2g + t_1u + t_2u

 

 

7.9 Схема связывания с помощью молекулярных орбиталей для МХ₆

Свойства симметрии s-, p- и d- орбиталей центрального атома, полученные из таблицы характеров точечной группы О_h были описаны ранее. Из этой таблицы можно сделать вывод, что они преобразуются в a_1g, t_1u и (e_g+t_2g) соответственно, и, зная это теперь возможно постороить диаграмму молекулярных орбиталей для МХ₆. На рис 7.14 показано как это может быть полностью завершено:

Рис. 7.13 Диаграмма МО для связывания в МХ6

 

 

Заключение

Основной задачей этой части было продемонстрировать, как можно строить схемы связывания с помощью молекулярных орбиталей, путём анализа симметрии участвующих наборов атомных орбиталей. Тем не менее, хотя общий результат заключается в том, что каждая орбиталь, которую можно идентифицировать имеет отличную от других энергию, рассмотрение симметрии не даёт никакой достоверной (надёжной) количественной информации, касающейся энергий этих орбиталей. В этом отношении ситуация подобная тому, что происходит в колебательной спектроскопии.

Но очевидным, однако, стал тот факт, что одинаковые представления возникали (появлялись, обнаруживались, находились) точно так же, как и в предыдущих частях, описывающих молекулярные колебания. Эта распространённая взаимосвязь является одним из наиболее интересных и используемых аспектов симметрии, и одной из главных задач этого пособия было продемонстрировать, как широко может распространяться подход, основанный на принципах симметрии.

Финальные (последние) упражнения, приведенные дальше? разработаны затем, чтобы объединить (организовать, обобщить_ материал, изложенный в этой части.