Р-орбитали центрального атома.

В изолированном атоме ксенона, валентные орбитали 5 p_x, 5 p_y и 5 p_z энергетически

Рис. 7.5

эквивалентны, и поэтомы трижды вырождены. Тем не менее. если этот атом поместить в центр плоско-квадратного окружений атомов фтора, как в XeF₄, вырождение частично снимается. Орбитали 5 p_x и 5 p_y остаются эквивалентными, но отличаются от 5 p_z. Это полностью очевидно из рисунка 7.5, где атомы фтора расположены на осях x и y, но ни один из них не лежит на оси z.

Теперь мы можем классифицировать р -орбитали в соответствии с представлениями, к которым они относятся в симметрии D_4h, и, помня, что орбитали p_x, p_y и p_z имеют ту же самую симметрию, что и функции и x, y и z, из таблицы характеров следует, что три 5 р орбитали преобразуются как Е_u + 2А_u в D_4h.

Эта таблица характеров также может использоваться для того, чтобы показать. Как 5 s и 5 d орбитали атома ксенона трансформируются в симметрии D_4h, но для того, чтобы получить эти представления, нам нужно знать математические функции, которые соответствуют s- и d- орбиталям.

s -орбитали центрального атома.

Все s –орбитали имеют сферическую симметрию, различаются только по количеству (числу) радиальных нод. Они невырожденные, и, поскольку уравнение, описывающее сферу (в Декартовых координатах) равно x ² + y ² + z ² = r ² (постоянная), мы будем искать вышеупомянутые функции в таблице характеров группы D_4h. Эта отдельно взятая таблица характеров не даёт эту функцию отдельно, но точнее содержит записи (x ² + y ²) и z ² каждая из которых по отдельности имеет симметрию А_1g, поэтому справедливо предположить, что сумма этих двух функций [(x ² + y ² + z ²)] также имеет симметрию А_1g, и s –орбитали в D_4h поэтому преобразуются в А_1g.

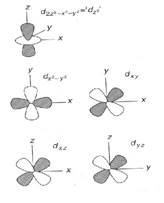
d -орбитали центрального атома.

На Рис. 7.6. показаны знакомые формы, связанные с пятью d -орбиталями. Математические

Рис. 7.6

функции, которые описывают формы d -орбиталей это (2z ²- x ² - y ²), (x ²- y ²), xy, xz и yz, и знаки этих функции относительно системы координат отвечают за patterns направление «+» и «-«знаков на разных частях этих орбиталей.

Последние четыре из этих образуют (формируют) похожие подписи которые определяют орбитали, такие как d_xy или d_yz, но функция (2z ²- x ² - y ²) может отличаться от них.На самом деле (фактически) правильная подпись для d -орбитали в более общем виде известна как d_z2. Во многих точечных группах функция z² имеет ту же самую симметрию, т.е. принадлежит к тому же самому представлению, что и функция (2z ²- x ² - y ²), и поэтому для удобства описание орбиталей может быть укорочено (упрощено) до «d_z2».

В некоторых точечных группах более высокой симметрии (особенно в O_h и T_d) необходима полная подпись (нижний индекс), и в таком виде она и приводится в таблице характеров, но в большинство таблиц характеров включен только z² –так как в D_4h.

Тем не менее, основной вывод, который может быть здесь сделан, состоит в том, что для центрального атома в окружении D_4h большая часть (часто?) пятикратного вырождения потеряна, с трансформацией вышеприведенных функций орбиталей в соответствии с представлениями A_1g, B_1g, B_2g и E_g.