Критерий знаков является одним из самых простых способов выявления существенных факторов. Он основан на N-статистике и служит для проверки гипотезы о равной вероятности положительного и отрицательного исходов для последовательности независимых событий. Результаты наблюдений (испытаний) независимы, если каждый их них не подвержен влиянию другого и не содержит информации о следующем. Если гипотеза о равной вероятности исходов независимых испытаний (их число равно n) P  =P
=P  не отвергается, то следует предположение, что исследуемый фактор не оказывает влияния на результат испытания.
не отвергается, то следует предположение, что исследуемый фактор не оказывает влияния на результат испытания.
Если количество положительных исходов равно 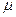 , то для проверки гипотезы H
, то для проверки гипотезы H 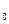 \p=0,5 (при конкурирующих H
\p=0,5 (при конкурирующих H 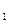 \p<0,5; H
\p<0,5; H 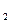 \p>0,5; H
\p>0,5; H 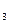 \p≠0,5) по таблице 6.6.
\p≠0,5) по таблице 6.6.
Определяют критические значения N (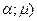 N(
N(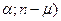 , соответствующие заданному уровню значимости.
, соответствующие заданному уровню значимости.
Пример: По данным источника, приведенным в таб.№1 требуется оценить влияние географического расположения района на производство фальшивых напитков l 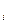 млн. в 199
млн. в 199
Таблица 3.17
Производство фальшивых напитков в РФ по районам,млн.дкл.
| 1. Центральные, южные и западные районы РФ
|
| Калиниградская область
| Волговятский
| Центральный
| Центрально-черноземный
| Северо-кавказский
| Приволжский
| Σ
|
| 2,0
| 6,0
| 26,0
| 3,4
| 7,8
| 12,4
|
|
| 1Северные и восточные районы РФ
|
| Уральские
| Западно-Сибирсикй
| Восточно-Сибирсикй
| ДАЛЬНЕвосточный
| Северный
| СЕВЕРО-западный
| Σ
|
| 13,6
| 9,7
| 4,9
| 6,5
| 3,4
| 1,4
|
|
Решение:
Чтобы можно было воспользоваться рассматриваемым критерием, область возможных значений производства напитков R по обеим группам районов делится на две равные части:
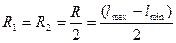 ,где
,где
R 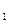 -область положительных значений производства напитков;
-область положительных значений производства напитков;
R 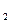 - область отрицательных значений
- область отрицательных значений
l 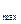 - значение максимального объема производства(центральный район
- значение максимального объема производства(центральный район
l 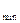 - значение минимального объема производства(северо-Западный район)
- значение минимального объема производства(северо-Западный район)
 =
= 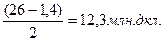
Количество положительных исходов для первой группы районов (больших граничного значения равно 12,3)равно 2 (центральный и Поволжский район); для второй группы районов количество положительных исходов равно 1 (Уральский район), поэтому 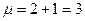 .Проверяется гипотеза H
.Проверяется гипотеза H 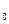 \p=0,5 при односторонней альтернативе H
\p=0,5 при односторонней альтернативе H 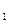 \p=0,5.Для этого случая критическое множество определяется равенством n
\p=0,5.Для этого случая критическое множество определяется равенством n  .пусть α=0,1,тогда по таблице N(0,1;3)=12Поскольку число районов также равно n=12 и таким образом n=N (0,1;3), то гипотеза о независимости объема производства фальшивых напитков от географического расположения районов отвергается. Следовательно, с доверительной вероятностью 0,9 место расположения района (в смысле принадлежности егок первой или второй группы влияет на объем производства фальшивой продукции) если же проводить процедуру отдельно для каждой группы районов, то окажется, что внутри групп расположение района не оказывает влияние на объем производства. Например, для первой группы области положительных r
.пусть α=0,1,тогда по таблице N(0,1;3)=12Поскольку число районов также равно n=12 и таким образом n=N (0,1;3), то гипотеза о независимости объема производства фальшивых напитков от географического расположения районов отвергается. Следовательно, с доверительной вероятностью 0,9 место расположения района (в смысле принадлежности егок первой или второй группы влияет на объем производства фальшивой продукции) если же проводить процедуру отдельно для каждой группы районов, то окажется, что внутри групп расположение района не оказывает влияние на объем производства. Например, для первой группы области положительных r 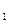 и отрицательных r
и отрицательных r 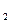 значений равны:
значений равны:
r 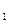 = r
= r 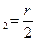
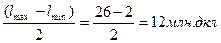
Количество положительных исходов для первой группы районов равно 2, поэтому 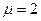 при числе районов первой группы n
при числе районов первой группы n 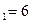 уровне значимости α=0, величина n
уровне значимости α=0, величина n 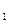
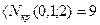 т.е., гипотеза об отсутствии влияния на объем производства фальшивых напитков расположения района; если он находится в первой группе не отвергается. А вариация объемов производства внутри групп объясняется другими факторами.
т.е., гипотеза об отсутствии влияния на объем производства фальшивых напитков расположения района; если он находится в первой группе не отвергается. А вариация объемов производства внутри групп объясняется другими факторами.

 =P
=P  не отвергается, то следует предположение, что исследуемый фактор не оказывает влияния на результат испытания.
не отвергается, то следует предположение, что исследуемый фактор не оказывает влияния на результат испытания.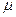 , то для проверки гипотезы H
, то для проверки гипотезы H 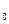 \p=0,5 (при конкурирующих H
\p=0,5 (при конкурирующих H 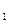 \p<0,5; H
\p<0,5; H 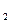 \p>0,5; H
\p>0,5; H 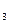 \p≠0,5) по таблице 6.6.
\p≠0,5) по таблице 6.6.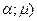 N(
N(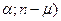 , соответствующие заданному уровню значимости.
, соответствующие заданному уровню значимости.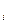 млн. в 199
млн. в 199 ,где
,где - значение максимального объема производства(центральный район
- значение максимального объема производства(центральный район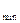 - значение минимального объема производства(северо-Западный район)
- значение минимального объема производства(северо-Западный район) =
= 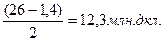
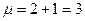 .Проверяется гипотеза H
.Проверяется гипотеза H  .пусть α=0,1,тогда по таблице N(0,1;3)=12Поскольку число районов также равно n=12 и таким образом n=N (0,1;3), то гипотеза о независимости объема производства фальшивых напитков от географического расположения районов отвергается. Следовательно, с доверительной вероятностью 0,9 место расположения района (в смысле принадлежности егок первой или второй группы влияет на объем производства фальшивой продукции) если же проводить процедуру отдельно для каждой группы районов, то окажется, что внутри групп расположение района не оказывает влияние на объем производства. Например, для первой группы области положительных r
.пусть α=0,1,тогда по таблице N(0,1;3)=12Поскольку число районов также равно n=12 и таким образом n=N (0,1;3), то гипотеза о независимости объема производства фальшивых напитков от географического расположения районов отвергается. Следовательно, с доверительной вероятностью 0,9 место расположения района (в смысле принадлежности егок первой или второй группы влияет на объем производства фальшивой продукции) если же проводить процедуру отдельно для каждой группы районов, то окажется, что внутри групп расположение района не оказывает влияние на объем производства. Например, для первой группы области положительных r 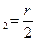
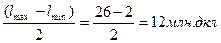
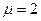 при числе районов первой группы n
при числе районов первой группы n 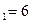 уровне значимости α=0, величина n
уровне значимости α=0, величина n 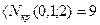 т.е., гипотеза об отсутствии влияния на объем производства фальшивых напитков расположения района; если он находится в первой группе не отвергается. А вариация объемов производства внутри групп объясняется другими факторами.
т.е., гипотеза об отсутствии влияния на объем производства фальшивых напитков расположения района; если он находится в первой группе не отвергается. А вариация объемов производства внутри групп объясняется другими факторами.


