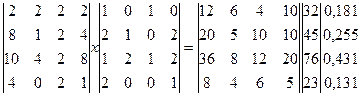Пример 7
Для оценки своей деятельности, выбора партнера по бизнесу фирма должна проводить независимую оценку своего положения на рынке. Рассмотрим метод экспертного моделирования ситуации фирм на рынке. Путем сравнения фирмы с конкурентами необходимо создать ранжированный ряд впереди ушедших фирм и следующих за вами. Численное соотношение множества сравниваемых фирм по шкале какого-нибудь критерия представляет собой рейтинг этого множества по шкале ранжирования. Эксперт осуществляет задание коэффициентов относительной важности парного сравнения на основе качественных (лингвистических)оценок, т.е. по критерию значимости –К, заполняет матрицу ||Z||сравниваемых фирм с установкой числовых значений: А) при сильном различии сравниваемых фирм Zij= 0, если фирма i хуже фирмы j; 1, если фирма i равносильна j; 2, если фирма лучше i фирмы j, Где i- номер строки матрицы, j- номер столбца матрицы. Б) при среднем различии ранжируемых фирм Zij= 0,5, если фирма i хуже фирмы j; 1,0, если фирма i равносильна j; 1,5, если фирма лучше i фирмы j, В) при незначительном различии сравниваемых фирм Zij= 0,8, если фирма i хуже фирмы j; 1,0, если фирма i равносильна j; 1,2, если фирма лучше i фирмы j, Фирмы i,j входят во множество М=1,2,…n ранжируемых фирм. Сравниваемые пары образуют матрицу ||Z||n x n значений этих соотношений, где n- число сравниваемых рекламных фирм. Например, проведем сравнение четырех отличительных фирм (М=1,2,3,4) по какому-то критерию –К.Эксперт, путем попарного сравнения фирм заполняет матрицу. 1 2 3 4 1 1 0 1 0 2 0,125 2 2 1 0 2 5 0,312 Z 4 2 0 0 1 3 0,185
По составленной матрице ||Z|| в качестве первого этапа производится «грубое» ранжирование путем построчного суммирования чисел
P По назначениям каждой строки образуется вектор P= В нашем примере рейтинговая шкала «грубого» ранжирования рекламных фирм выглядит следующим образом: 1 4 2 3
0,125 0,185 0,312 0,376 Анализ оси R позволит определить весовые коэффициенты С Если рейтинг определяют несколько экспертов, то итоговый вектор значений P необходимо усреднить по правилам обработки экспертных оценок. На втором этапе «тонкого» ранжирования осуществляется перемножение матрицы ||Z|| саму на себя с получением новой матрицы Z1=||Z||х||Z|| С матрицей ||Z||1проводится аналогичная работа по суммированию строк и построение нового ряда значений векторов P и R.При «тонком» ранжировании весовые коэффициенты принимают более четкие значения и более утвердительно выглядит рейтинг фирм. Матрица «тонкого» ранжирования для нашего примера выглядит так: Z
«Тонкий» рейтинг первого уровня фирм стал выглядеть следующим образом: 4 1 2 3
0,129 0,148 0,277 0,444
Из сравнения шкал R видно: лидерство сохранилось, аутсайдеры, находясь близко друг от друга, поменялись местами. Матрица второго уровня «Тонкого» ранжирования примет вид: Z Рейтинговая шкала второго уровня выглядит так: 4 1 2 3
0,131 0,181 0,255 0,431
Таким образом, порядок рейтинга фирм стабилизируется и утверждаются весовые коэффициенты - С.Чем больше производить умножение полученных матриц на исходную ||Z||, тем точнее значения весов P и весовых коэффициентов – С.Практически перемножение матриц можно закончить на 4 этапе.
|

 C
C 
 = 3 1 2 1 2 6 0,376
= 3 1 2 1 2 6 0,376 16 1
16 1 по каждой строке матрицы. Далее производится суммирование чисел матрицы
по каждой строке матрицы. Далее производится суммирование чисел матрицы  и е определение веса сравниваемой фирмы в виде коэффициента
и е определение веса сравниваемой фирмы в виде коэффициента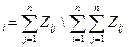
 , который представляет собой численное соотношение (рейтинги) сравниваемых фирм по критерию - К.На основании вектора P строится рейтинговая шкала значимости рекламных фирм. Если веса объектов соотносятся как P
, который представляет собой численное соотношение (рейтинги) сравниваемых фирм по критерию - К.На основании вектора P строится рейтинговая шкала значимости рекламных фирм. Если веса объектов соотносятся как P 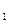 >P
>P 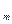 >…>P
>…>P  , то ряд предпочтений сравниваемых фирм выглядит I>m>…>n и их рейтинги соответственно r(i)>r(m)>…> r(n) на шкале рейтинга R.
, то ряд предпочтений сравниваемых фирм выглядит I>m>…>n и их рейтинги соответственно r(i)>r(m)>…> r(n) на шкале рейтинга R.
 R
R , которые показывают, во сколько раз фирма I весомее J на шкале R по выбранному критерию - К или на сколько пунктов фирма I опережает или отстает от фирмы j. Таким образом, рейтинговый порядок фирм выглядит 3>2>4>1 с коэффициентами: фирма 3 лучше 2 в С32=0,376/0,312=1,205 или на 20,5%, фирма 2 лучше 4 в С24=0,312/0,185=1,686 или на 68.6% фирма 4 лучше 1 в С 41=0,185/0,125=1,48 или на 48% Лидер 3 лучше аутсайдера 1 в С31=0,376/0,125=3,008.
, которые показывают, во сколько раз фирма I весомее J на шкале R по выбранному критерию - К или на сколько пунктов фирма I опережает или отстает от фирмы j. Таким образом, рейтинговый порядок фирм выглядит 3>2>4>1 с коэффициентами: фирма 3 лучше 2 в С32=0,376/0,312=1,205 или на 20,5%, фирма 2 лучше 4 в С24=0,312/0,185=1,686 или на 68.6% фирма 4 лучше 1 в С 41=0,185/0,125=1,48 или на 48% Лидер 3 лучше аутсайдера 1 в С31=0,376/0,125=3,008.
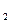 =Z
=Z