Для независимых случайных величин корреляционный момент 0 !
Системы случайных величин (n > 2) Закон распределения случайной величины - полная ее характеристика. F(x1, x2,.., xn) = P((X1 < x1) (X2 < x2)..(Xn < xn)) - функция распределения f(x1, x2,.., xn) = F1(x) = F[x1, Условная плотность распределения f(x1,..,xk\ xk+1,..,xn) = Для независимых случайных величин f(x1, x2,.., xn) = f(x1)..f(xn) Вероятность попадания случайной точки (x1,.., xn) в пределы n - мерной области D: P((x1, x2,.., xn) Числовые характеристики системы нескольких случайных величин 1) n математических ожиданий m1, m2,..,mn 2) n дисперсий D1, D2,..,Dn 3) n(n-1) корреляционных моментов kij = (при i = j) имеем дисперсии Di = kii = Корреляционный момент описывается ковариационной (корреляционной) матрицей [kij] = [rij] =
Двумерный нормальный закон распределения Для двумерного закона (x1, x2) или (x,y) имеем f(x,y) = при r = 0 (то есть величины не коррелированы) f(x,y) = То есть для нормального закона справедливо утверждение: Если случайные величины некоррелированы, то они независимы. Законы распределения, связанные с нормальным 1. Если
Сумма квадратов случайных величин имеет 2. Величина t = f(t) =
|
- плотность распределения
]
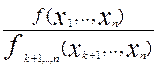
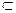D) = 
dx1... dxn
= Dx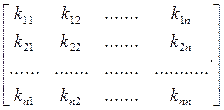
- симметричнаядиагональная матрица
- нормированная ковариационная матрица
= f(x)f(y)
- распределение
- случайная, нормально распределенная величина (0,1) математическое ожидание = 0, дисперсия = 1, то
= 
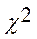
- распределение.
имеет t - распределение Стьюдента.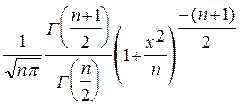
, где Г(p) = 
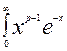dx - гамма -функция
