Робастные оценки
Реальные ряды ошибок измерений достаточно хорошо описываются распределениями с тяжелыми хвостами или Пусть измерительное устройство с вероятностью (1 - P(z) = а дисперсия выборочного среднего M При Таким образом, дисперсия выборочного среднего Задача теории робастного оценивания: Найти такие оценки параметров, которые были бы нечувствительными к отклонениям ошибок от нормального закона (наличие выбросов и так далее), но не слишком бы проигрывали в эффективности по сравнению с оценками МП, если закон распределения ошибок - нормальный. Считается, что потери 5-10% эффективности - вполне приемлемая плата за устойчивость оценок. Наиболее удачным считается метод помехоустойчивого оценивания, основанный на приеме максимального правдоподобия - M-оценки.
|

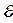 - загрязненными распределениями.
- загрязненными распределениями.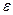 ) работает в основном режиме, при котором ошибка измерений имеет распределение P0(z) с дисперсией
) работает в основном режиме, при котором ошибка измерений имеет распределение P0(z) с дисперсией 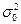 , и с небольшой вероятностью
, и с небольшой вероятностью 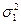 . Тогда общее распределение ошибок имеет вид
. Тогда общее распределение ошибок имеет вид ,
, , где Сn - выборочное средние, равна
, где Сn - выборочное средние, равна 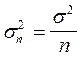 , где
, где 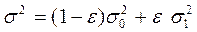 .
.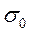 =1,
=1, 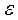 = 0.1,
= 0.1,  = 3 имеем
= 3 имеем  = 1.8, а при
= 1.8, а при  = 5,
= 5, 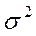 = 3.4.
= 3.4.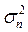 быстро растет с увеличением дисперсии
быстро растет с увеличением дисперсии  , а при
, а при 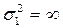 (когда H - распределение Коши) выборочное среднее становится несостоятельной оценкой параметра c* (то есть не сходится по вероятности к c*).
(когда H - распределение Коши) выборочное среднее становится несостоятельной оценкой параметра c* (то есть не сходится по вероятности к c*).


