Проверка гипотез.
При проверке гипотез подвергается испытанию некоторая гипотеза H0 в сравнении с одной или большим числом альтернативных гипотез H1, H2,....
Пусть известна плотность распределения вероятности 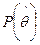 для оценки для оценки 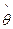 (несмещённой). Как сильно должна отличаться величина (несмещённой). Как сильно должна отличаться величина 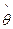 от от 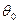 , предполагаемого истинного значения , предполагаемого истинного значения 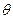 , чтобы эта гипотеза была отвергнута? , чтобы эта гипотеза была отвергнута?
Если гипотеза
В силу симметрии
a - уровень значимости. a << 1 a=0,05; 0,01 и т.д.
Таким образом при При
Простейший случай, когда проверяются две гипотезы: 1. Н0: х – истинное значение случайной величины (нулевая гипотеза) 2. Н1: х – не является истинным значением (альтернативная гипотеза) Пусть проверяются гипотезы о значении параметра H0: H1:
Решение принимается следующим образом: считая, что нулевая гипотеза верна, вычисляют статистику по экспериментальной выборке и проверяют, попадает ли вычисленное значение в область принятия гипотезы. Если – нет, то гипотеза Н0 отвергается, принимается гипотеза Н1 Если – да, то принимается гипотеза Н0.
Ошибки при проверке гипотез: Ошибка первого рода: гипотеза верна, но отвергается. Ошибка второго рода: гипотеза не верна, но принимается.
Ошибка первого рода связана с тем, что Уменьшить её можно уменьшая Ошибка второго рода связана с вероятностью принятия гипотезы Н0, тогда как на самом деле имело место гипотеза Н1.
Вероятность Вероятность Уменьшение ошибки первого рода ведёт к увеличению ошибки второго рода и наоборот при заданном объёме выборки.
Единственный способ уменьшить одновременно обе ошибки – увеличение объёма выборки.
Пример: проверка гипотезы относительно среднего. Пусть некоторая случайная переменная процесса Х имеет среднее значение Проверяем гипотезу Н0: случайная переменная имеет прежнее среднее Альтернативная гипотеза: Н1 Для двустороннего критерия t гипотеза Н0 принимается, если В противном случае принимается Н1.
Принимается Н0. Для одностороннего критерия (если бы проверяли гипотезу
Гипотезу Н0:
Среднее по ансамблю сравнивается с Правила принятия решения приведены в таблице:
Пример: Проверка гипотезы относительно среднего. Калибровка термометров сопротивления. Стандартный термометр показывает 1000 мВ. Показания термометров:
Можно ли считать отклонения случайными, или на показания термометров воздействовал некий фактор? Гипотеза: Н0: Дисперсия Используется критерий Выбираем
6>5.
На уровне значимости
Проверка гипотез относительно средних по ансамблю двух продуктов (двух переменных).
Предполагается, что генеральная совокупность имеет нормальное распределение. nA – число наблюдений из выборки А. nВ – число наблюдений из выборки В. t вычисляется для Если вычисляется разность > правой части, то гипотеза принимается, в противном случае отвергается.
|

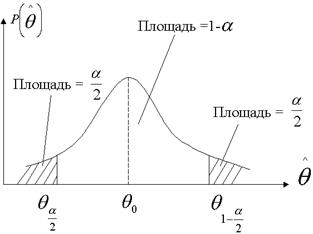
 верна, то
верна, то 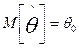 .
.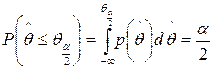 .
. .
.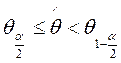 гипотеза принимается.
гипотеза принимается.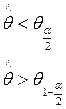 - гипотеза отвергается.
- гипотеза отвергается.
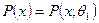
 .
.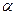 .
.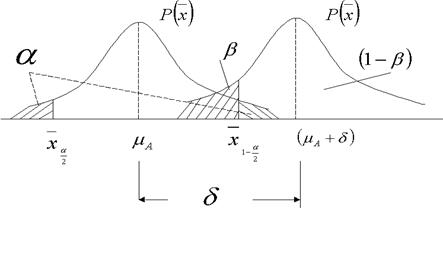
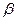 - вероятность не обнаружить разницу, когда она существует.
- вероятность не обнаружить разницу, когда она существует.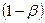 называется мощностью критерия и определяет вероятность принятия решения Н0, когда гипотеза является ложной. С увеличением
называется мощностью критерия и определяет вероятность принятия решения Н0, когда гипотеза является ложной. С увеличением 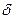 ,
, 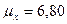 . Для выборки объёма
. Для выборки объёма 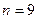 получено
получено 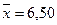 и
и  (
(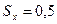 ).
). . Пусть уровень значимости
. Пусть уровень значимости 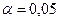 .
.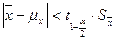 .
.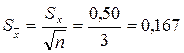
 для
для  степеней свободы и
степеней свободы и 
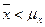 ) следовало бы взять
) следовало бы взять 
 . 0,30<0,31
. 0,30<0,31

 предполагается известным.
предполагается известным.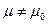
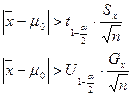
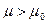
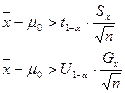
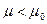
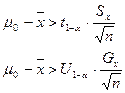
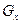 неизвестна.
неизвестна.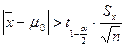 .
.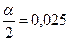 .
. 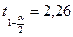 .
.
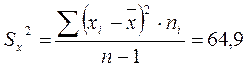
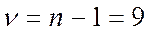
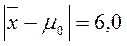
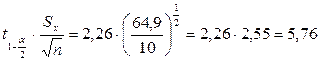

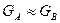 оба неизвестны
оба неизвестны
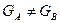 оба неизвестны
оба неизвестны
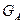 и
и  известны
известны
 т.к. 2 случайные величины
т.к. 2 случайные величины 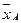 и
и 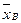 , то дисперсия = сумме дисперсии.
, то дисперсия = сумме дисперсии.

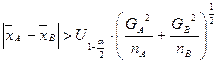 нормальное распределение
нормальное распределение
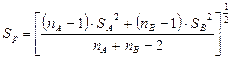
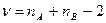
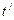 -значение
-значение 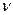 степ. свободы
степ. свободы
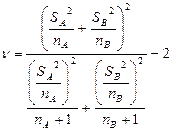
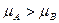
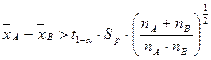


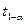 для
для  степеней свободы.
степеней свободы.


