Построение линейной регрессионной модели с одной независимой переменной.
Одной из основных задач обработки данных является установление функциональной зависимости между переменными (параметрами) исследуемого процесса. Зачастую такие зависимости не очевидны, или слишком сложны. В таком случае ставится задача аппроксимации функциональной связи по эмпирическим данным. Эта задача решается с помощью регрессионного метода, который был назван известнейшим специалистом в области обработки данных Тьюки методом века. Аппроксимацией называется подбор математического выражения, описывающего связь между экспериментальными данными. Само математическое выражение называют уравнением регрессии (регрессией), а соответствующую кривую - линией регрессии [1]. Простейшей регрессионной зависимостью является линейная. Если между переменными существует линейная функциональная связь, то результаты измерений будут концентрироваться около прямой, отражающей эту зависимость. Отклонения от прямой вызваны погрешностью измерений. В случае двух переменных одна из них - X рассматривается как независимая и называется фактором или предиктором, вторая переменная Y является зависимой и называется откликом. Таким образом,уравнение Y относительно X - уравнение регрессии (говорят что Y регрессирует на X). В случае линейной модели уравнение регрессии имеет вид:
где b0 и b1 параметры модели; e - остаточный член, обусловленный влиянием погрешностей измерений, случайных вариаций Y и погрешностью модели. Погрешность модели возникает в случае замены какой - либо более сложной модели линейной зависимостью. Оценки параметров модели (b0 и b1) находятся по результатам наблюдений. Модель (1) является линейной первого порядка. Порядок модели определяется наивысшей степенью предиктора. Так модель
является линейной (относительно параметров b) третьего порядка.. В результате построения модели находятся оценки параметров b0 и b1 Уравнение регрессии, соответствующее уравнению (1), имеет вид
где МНК - оценки параметров получаются минимизацией суммы квадратов отклонений от «истинной» линии.
где n - число независимых наблюдений величин Хi и Yi Получены следующие МНК оценки параметров b0 и b1[2]
где
|

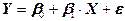 , (1)
, (1)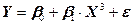 (2)
(2)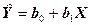 , (3)
, (3)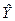 - расчетное или прогнозируемое значение Y для данного X.
- расчетное или прогнозируемое значение Y для данного X.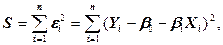
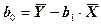
 , (5)
, (5)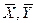 - средние значения наблюдаемых величин X и Y. Подставляя оценки (5) в уравнение (3), можно вычислить «прогнозируемые» значения
- средние значения наблюдаемых величин X и Y. Подставляя оценки (5) в уравнение (3), можно вычислить «прогнозируемые» значения 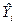 и найти остатки
и найти остатки 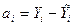 . Для правильно построенной модели сумма остатков равна 0.
. Для правильно построенной модели сумма остатков равна 0.


