Исследование уравнений регрессии.
Для наблюденных пар {Xi, Yi} было построено уравнение регрессии
Уравнение (1) можно представить в виде.
Возведя в квадрат обе части уравнения (2) и просуммировав все уравнения по i: i=1,..., n, получим [2]
В уравнении (3) сумма Сумма Сумма
Качество построенной модели тем выше, чем больше сумма квадратов, обусловленная регрессией, превосходит сумму квадратов остатков относительно регрессии! Так как сумма квадратов отклонений пропорциональна дисперсии случайной величины, то уравнение (3) называется основным уравнениемдисперсионного анализа. В статистике исследуются средние квадраты остатков, которые получаются делением их суммы на число степеней свободы. Под числом степеней свободы некоторой статистики понимается разность между числом наблюдений и числом параметров, определенных по этим наблюдениям [3]. Сумма квадратов отклонений относительно среднего имеет (n-1) степеней свободы [3]. С учетом выше изложенного строится таблица дисперсионного анализа.
Если наблюдения независимые, а их погрешности подчиняются нормальному распределению, то отношение Задавая уровень значимости a, и сравнивая Fвыч.=
b0:
b1: где S - средний остаток относительно регрессии (остаточная дисперсия). Для проверки гипотезы о равенстве параметра b0 некоторой заданной величине b00 (H0: b0=b00) вычисляется величина t
Вычисленное значение t сравнивается с табличным Для проверки гипотезы о равенстве параметра b1 некоторой величине b10 вычисляется статистика
и сравнивается с табличным значением Решение о принятии гипотезы H0: b1=b10 принимается при t выч.< t табл. Оценка стандартного отклонения вычисленного значения
СКО
Доверительные интервалы для
Литература 1. Химмельблау Д. «Анализ процессов статистическими методами.» Издательство «Мир», Москва, 1973, 957 стр. 2. Венцель Е.С. «Теория вероятности.» 3. Дрейпер и Смит. «Прикладной регрессионный анализ.» 4. Бокс, Дженкинс. «Анализ временных рядов.» 5. Дженкинс, Бокс. «Спектральный анализ и его приложения.» 6. П. Тойберт. «Оценка точности результатов измерений.» 1988. 7.Пустыльник Е. И. «Статистические методы анализа и обработки наблюдений.» «Наука.» Москва. 1968. 8. Гмурман В. Е. «Руководство к решению задач по теории вероятности и математической статистике.» 1975.
Содержание 1. Основные задачи обработки измерений. Стр. 2 2. Основные понятия теории вероятностей (краткий обзор). Стр. 5 3. Числовые характеристики системы двух случайных величин. Стр. 11 4. Критерии качества оценок. Стр. 13 5. Метод максимального правдоподобия. Введение в помехоустойчивое оценивание. Стр. 15 6. Получение интервальных оценок. Стр. 20 7. Проверка гипотез. Стр. 24 8. Проверка гипотез относительно средних. Стр. 27 9. Проверка гипотез для дисперсий. Стр. 32 10. Построение линейной регрессионной модели с одной независимой переменной. Стр. 34 11. Исследование уравнений регрессии. Стр. 35 10. Литература. Стр. 38
|

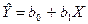 . В каждой точке Xi получено отклонение «предсказанного» значения
. В каждой точке Xi получено отклонение «предсказанного» значения 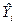 от наблюденного Yi: Это отклонение (остаток) можно представить в виде:
от наблюденного Yi: Это отклонение (остаток) можно представить в виде: (1)
(1) (2)
(2)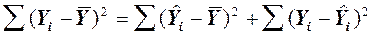 (3)
(3) является суммой квадратов отклонений зависимой переменной относительно среднего значения
является суммой квадратов отклонений зависимой переменной относительно среднего значения  .
. - представляет собой сумму квадратов отклонений предсказанных значений относительно среднего значения независимой переменной (сумма квадратов, обусловленная регрессией) и характеризует угол наклона линии регрессии.
- представляет собой сумму квадратов отклонений предсказанных значений относительно среднего значения независимой переменной (сумма квадратов, обусловленная регрессией) и характеризует угол наклона линии регрессии. - сумма квадратов отклонений i - го наблюдения величины Y - oт ее предсказанного значения. Таким образом, уравнение (3) можно выразить следующим образом:
- сумма квадратов отклонений i - го наблюдения величины Y - oт ее предсказанного значения. Таким образом, уравнение (3) можно выразить следующим образом:



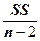
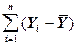
 подчиняется F - распределению с числом степеней свободы g1 =1, g2 =n - 2
подчиняется F - распределению с числом степеней свободы g1 =1, g2 =n - 2 с табличным значением F - распределения, можно проверить гипотезу о значимости отличия MSрег от S (При этом вероятность ошибки будет равна a. В ППП «STATISTICA» уровень вероятностей ошибки -P выводится на экран). 100×(1-a)%-е доверительные интервалы для коэффициентов b0 и b1 определяются выражением [2]:
с табличным значением F - распределения, можно проверить гипотезу о значимости отличия MSрег от S (При этом вероятность ошибки будет равна a. В ППП «STATISTICA» уровень вероятностей ошибки -P выводится на экран). 100×(1-a)%-е доверительные интервалы для коэффициентов b0 и b1 определяются выражением [2]: (3)
(3) (4)
(4) (4)
(4) . Если t вычисл. < t таблич., гипотеза H0 принимается.
. Если t вычисл. < t таблич., гипотеза H0 принимается. (5)
(5)
 (при X=X0) равна [3]
(при X=X0) равна [3] (6)
(6) (7)
(7)


