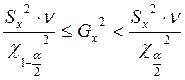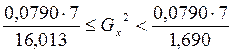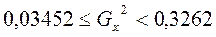Получение интервальных оценок
Доверительный интервал с заданной вероятностью накрывает теоретический параметр (истинное значение параметра). Доверительный интервал вычисляется по данным из некоторой выборки. Фиксированная величина параметра заключена между границами интервала, называемыми доверительными пределами, с некоторой заданной степенью достоверности, называемой доверительной вероятностью.
Общая процедура получения интервальной оценки: 1. Некоторое вероятностное утверждение записывается в математических символах, содержащих рассматриваемый параметр ансамбля. 2. Аргумент преобразуется так, чтобы параметр ансамбля был заключён между статистиками, которые модно вычислить по выборке.
úú.1. Получение интервальной оценки для среднего (неизвестного) по ансамблю mx случайной величины Известно, что статистика 1) 2)
3)
Если индексы n и b симметричны относительно t=0, то интервал по t симметричен.
Чтобы сделать площадь под кривой распределения вне интервала раной Таким образом После того как получена выборка, Симметричный доверительный интервал для среднего по ансамблю можно получить, преобразуя аргумент в
Доверительная вероятность для интервала, заданного неравенством
2. Если известна величина
Если
3. Доверительный интервал для дисперсии по ансамблю 4.
 (ni – число повторений xi) подчиняется c2 – распределению с (n-1) степенями свободы, (ni – число повторений xi) подчиняется c2 – распределению с (n-1) степенями свободы, 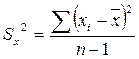 (при ni=1), (при ni=1),
Следовательно,
Поэтому (подставив c2 в
Преобразовав это выражение, получим
При
Аналогично можно рассмотреть другие средние по ансамблю, если известно распределение их выборочных оценок. Если такие распределения не известны, необходимо воспользоваться неравенством Чебышева.
Пример: Доверительные интервалы для среднего значения и дисперсии по ансамблю. Дана выборка:
Х (см3)- определение объёма.
n=n-1=7
Для 95% вероятности и для симметричного интервала (1-a=0,95; a/2=0,025) Находим t0,975=2,36
Симметричный доверительный интервал, согласно
Доверительный интервал для
|

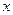 , распределённой по нормальному закону. Используем выборочное среднее
, распределённой по нормальному закону. Используем выборочное среднее  и выборочную дисперсию Sx2.
и выборочную дисперсию Sx2. - подчиняется распределению Стьюдента. Поэтому можно сделать вероятностные утверждения относительно величины t:
- подчиняется распределению Стьюдента. Поэтому можно сделать вероятностные утверждения относительно величины t: ;
;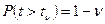 ;
;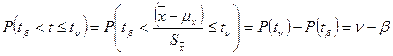
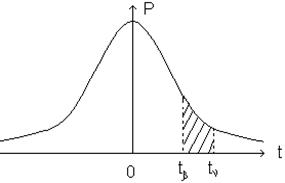

 a/2 + a/2 = a, было положено b=1-n; таким образом b=1-a/2.
a/2 + a/2 = a, было положено b=1-n; таким образом b=1-a/2.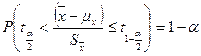

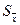 рассматриваются как фиксированные числа. Однако сам интервал является случайной переменной.
рассматриваются как фиксированные числа. Однако сам интервал является случайной переменной.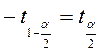
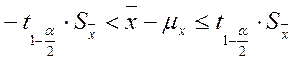
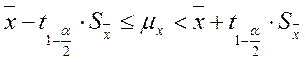

 и известен какой либо (U) закон распределения случайной величины (чаще всего это нормальный закон т.к. из центральной предельной теоремы следует, что выборочное среднее подчиняется нормальному закону), то можно построить доверительные интервалы для mx.
и известен какой либо (U) закон распределения случайной величины (чаще всего это нормальный закон т.к. из центральной предельной теоремы следует, что выборочное среднее подчиняется нормальному закону), то можно построить доверительные интервалы для mx.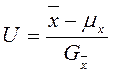 .
.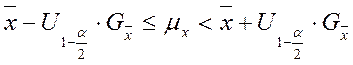 .
.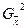 случайной величины можно найти, используя c2 распределение
случайной величины можно найти, используя c2 распределение
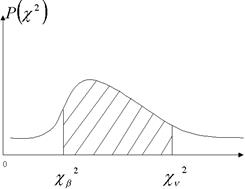
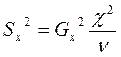 n=n-1.
n=n-1.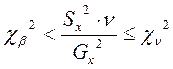
 .
. ;
; 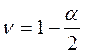
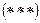
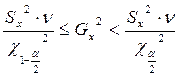 с доверительной вероятностью 1-a.
с доверительной вероятностью 1-a.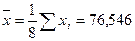
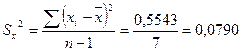
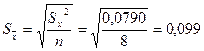

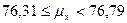 с вероятностью 0,95.
с вероятностью 0,95.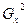 с a=0,05 имеет вид
с a=0,05 имеет вид