Критерии для сравнения средних значений.
Рассмотрим (для примера) первый случай.
Предположим, что имеются выборки случайных переменных А и В, распределённых по нормальному закону с указанными ниже средними значениями и дисперсиями.
Можно вычислить следующие выборочные статистики:
Выборочные Их разность (сумма дисп. средн.) Если Если эти гипотезы справедливы, то разность
Известно, что если из нормально распределённой совокупности производится k выборок, каждая из которых обладает одной и той же дисперсией (но не обязательно одним и тем же средним), то объединённая оценка дисперсии
(Если С учётом этого находим оценку для
Таким образом статистика
имеет t распределение с
Пример: сравнение двух средних. Два разных сорта бензина (октановые числа 90 и 94) использовались для определения числа пройденных километров на литр бензина. (Пробег по одному и тому же маршруту). – количество пробегов – по пяти.
|
; 
; 
; 
.
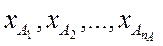
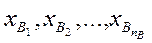
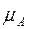
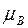
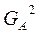
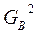
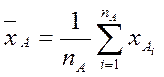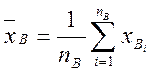
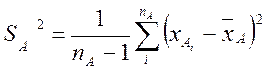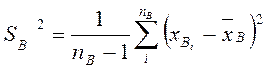
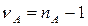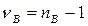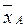и 
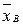распределены по нормальному закону 
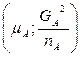и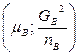 
.
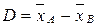также распределена нормально 
.
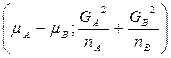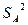значимо не отличается от 
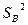проверяются гипотезы 
; 
.
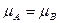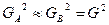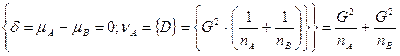
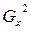равна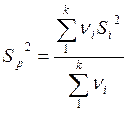
\ (взвешенное среднее) 
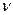- число степеней свободы
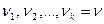, то получим 
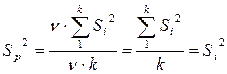, то есть среднее.)
.
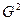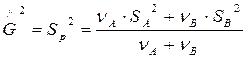
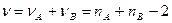
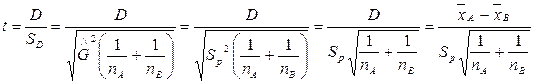; следовательно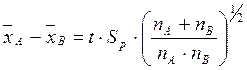
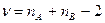степенями свободы. Если t значимо отлично от нуля, следует считать, что 
.
