Методы оценивания параметров
Наиболее часто используются 3 метода: 1. метод максимального правдоподобия; 2. метод моментов; 3. оценивание по Байесу. Мы будем рассматривать только метод максимального правдоподобия.
Метод максимального правдоподобия (предложен Фишером) Пусть P(x; Q1, Q2,.., Qn) - плотность распределения случайной величины X, Qi - параметр функции распределения. Считается, что вид плотности распределения функции - известен. Пусть имеем выборку из n независимых наблюдений из одного и того же распределения. Совместную плотность при этом можно записать так gn(X \ Q) = gn(x1, x2,..,xn \ Q) = f(x1 \ Q) f(x2 \ Q).... f(xn \ Q) Совместное распределение наблюдений, рассматриваемое как функция неизвестного параметра Q, называется функцией правдоподобия (ФП) выборки. gn(X \ Q) = f(x1 \ Q) f(x2 \ Q).... f(xn \ Q) Те значения выборки Q, для которых функция правдоподобия достигает максимума (так как события x1, x2,..,xn - уже произошли, то они имеют максимальную вероятность, равную 1!), называются оценками максимального правдоподобия. ОМП - оценки максимального правдоподобияобладаютследующими свойствами: n оценки асимптотически несмещенные n асимптотически нормальные; n асимптотически эффективные. Более удобно работать с логарифмической функцией правдоподобия. Переход к логарифмической функции правдоподобия возможен потому, что значения аргументов, максимизирующие функцию и ее логарифм - совпадают (*) ln(X \ Q) = lnng(X \ Q) = Если функция правдоподобия достаточно гладкая, то есть имеет 1-ую и 2-ую производные, то ее максимум ищется приравниванием нулю частных ее производных по каждому из параметров Qi.
Или, что то же самое, (**) Пример: оценивание параметров функции правдоподобия. f(x,Q1, Q2) = g(Q1, Q2 \ x1, x2,..,xn ) = (***) lng = L =-nln(Q2 (****) Решение системы (****) дает следующие оценки:
E[
В (***) первый член МНК был разработан К. Гауссом в начале 19 века. Основное его достоинство - простота реализации и ясный физический смысл. МНК широко применяется в различных задачах, связанных с построением математических моделей. Параметры моделей подбираются таким образом, чтобы минимизировать сумму квадратов отклонений вычисленных по модели значений от наблюденных, и так далее (такая же задача ставится при обработке измерений).
|

 (! асимпто-тическая несмещенность ОМП вовсе не означает что оценки всегда не смещены);
(! асимпто-тическая несмещенность ОМП вовсе не означает что оценки всегда не смещены);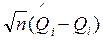

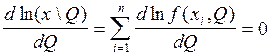

 Опыты независимы!!
Опыты независимы!! =
= 
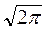 ) -
) - 
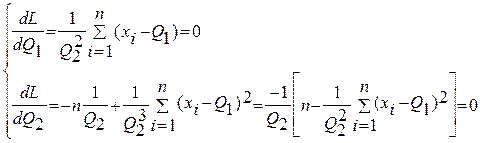
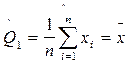

 ] =
] =  , где
, где 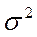 - дисперсия - параметр закона распределения
- дисперсия - параметр закона распределения - выборочная дисперсия - несмещенная оценка дисперсии
- выборочная дисперсия - несмещенная оценка дисперсии
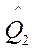 - смещенная оценка параметра
- смещенная оценка параметра  - дисперсии
- дисперсии не влияет на положение максимума, так как
не влияет на положение максимума, так как  - параметр масштаба, а не сдвига. Второй же член входит в L со знаком (-). Поэтому для максимизации функции правдоподобия необходимо минимизировать выражение
- параметр масштаба, а не сдвига. Второй же член входит в L со знаком (-). Поэтому для максимизации функции правдоподобия необходимо минимизировать выражение  , то есть сумму квадратов отклонений случайных величин
, то есть сумму квадратов отклонений случайных величин  от своего математического ожидания (от среднего). Это обстоятельство, по существу, - теоретическое обоснование метода наименьших квадратов.
от своего математического ожидания (от среднего). Это обстоятельство, по существу, - теоретическое обоснование метода наименьших квадратов.


