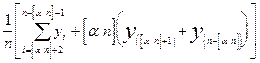М - оценкиПусть x1, x2,..,xn - последовательность независимых, одинаково распределенных случайных величин, имеющих непрерывную плотность вероятности f(x - Q), где Q - параметр сдвига. Логарифм функции правдоподобия можно записать lоg(Q) = L(Q) = Согласно методу МП требуется максимизировать lоg(Q) или, что то же самое, минимизировать K(Q) = Предположим, что минимум можно найти путем дифференцирования и решения уравнения K (*) Решение этого уравнения, минимизирующее K(Q) называется оценкой максимального правдоподобия или М - оценкой параметра Q и обозначается Приведем учебные примеры распределения погрешностей и соответствующие им оценки максимального правдоподобия: 1. нормальное распределение
p = -lnf(x) = Уравнение (*) имеет вид 2. двойное экспоненциальное распределение
Уравнение (*) имеет вид Хьюбер, используя строгое определение помехоустойчивости, нашел общий вид функций:
Эти функции минимизируют асимптотическую дисперсию V(T) оценок, где T- класс точности. Использование этих функций приводит к следующим оценкам параметров сдвига: 1. Исходная выборка упорядочивается: y(1) Отбрасывается 100% Ct(
2. Введены в начале 40-х годов К.П. Винзором [ Cw (
|
, где p(x) = -lоf(x)
.
(Q) = 0, то есть поиском соответствующего значения параметра сдвига Q, которое удовлетворяет условию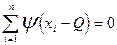
, где 
, при m = 0 и 
=1 
; 
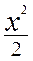и дает оценку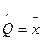 
; p = -lnf(x) = | x |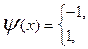
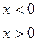
дает оценку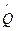 
, равную медиане.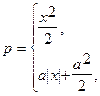
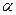- усеченные оценки.
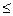y(2)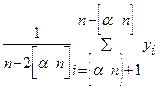 
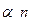] крайних значений не отбрасываются, проектируются в ближайшую точку оставшейся части упорядоченной выборки
) = 
