Случайная величина и ее характеристикиВероятность суммы двух независимых случайных событий равна сумме вероятностей этих событий P(A+B) = P(A) + P(B); P( События называются зависимыми, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий P(A*B) = P(A)*P(B) Обобщая, P(Пai) = ПP(Ai)
Для зависимых событий: P(A*B) = P(A)*P(B/A) P(A*B) = P(B)*P(A/B) Основные законы распределения случайных величин. Биномиальное распределение Вероятность того, что при проведении n независимых опытов, событиеА появится ровно m раз. Вероятность появления А в одном опыте равна p, вероятность появления равна q; (q = 1-p) Pm,n = Равномерное распределение
E[x] = mx = Нормальный закон распределения (закон Гаусса)
f(x) =
Действительно, можно показать, что M[x] = D[x] = Нормированная нормальная случайная величина t t = Ф[x] - табулирована P(a Закон редких событий (закон Пуассона) Pm =
|
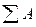i) = 
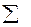P(Ai)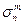
pmqn-m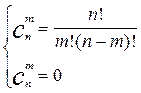 
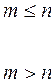
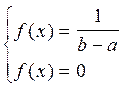
F(x) =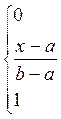 
; 
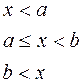
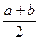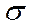
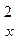= Dx = µ2 =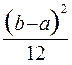 
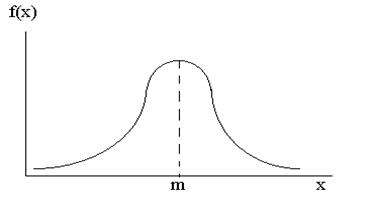
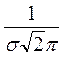
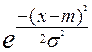, m - математическое ожидание
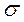- средне квадратичное отклонение
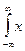f(x)dx =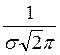 
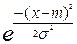dx = m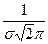
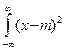
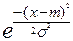dx =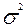 
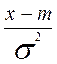; Ф[x] = 
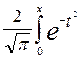dt - функция Лапласа или интеграл вероятности
x < b) = 
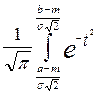dt =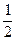 
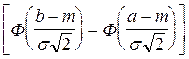
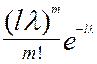, Pm - вероятность того, что на отрезок длинной l попадает ровно m точек, 
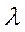- математическое ожидание числа точек, приходящихся на одну длину (средняя плотность), 
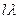- среднее число точек на отрезке.
