ИЗОБРАЖЕНИЯ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. Найти изображение единичной функции Хевисайда
при
2. Найти изображение функции
при
 .
Итак Аналогично можно получить следующие изображения:
4. Найти изображение функции
  
5.Найти изображение функции
 
так как В таблице 1 приведены изображения некоторых простейших оригиналов Таблица 1
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 1с) Линейность. Пусть функции
Заметим, что для Справедливо и обратное утверждение: если
Здесь также важно, что Используя свойство линейности, можно значительно проще найти изображения тригонометрических и гиперболических функций, например: а)
С) Теорема подобия Для любого
Доказательство: Пусть
Следствие:
|
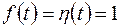. Найдем 
, пользуясь определением:
,
.
.
.
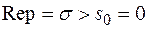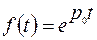В результате получим уравнение для нахождения 
:
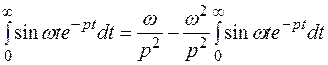, или
, откуда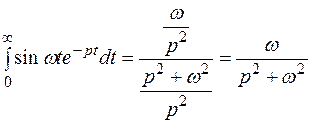
.
.
, 
, 
.
.
.
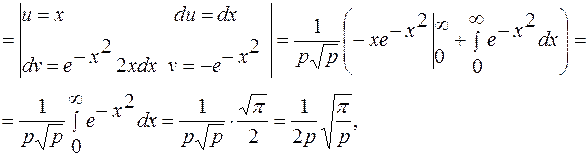
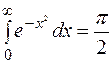интеграл Пуассона.
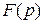
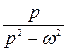
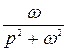
являются оригиналами. Соответствующие им изображения обозначим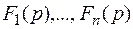 
. Тогда для любых комплексных чисел 
, 
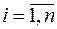функция 
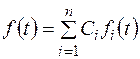также является оригиналом с изображением 
и справедливо равенство:
существенно, что все 
, 
является оригиналом, а слагаемые 
и 
не являются.
, 
является изображением, а слагаемые 
и 
не являются.
итак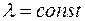
имеет место соотношение
