ВВЕДЕНИЕ. на присуждение денежных поощрений
на присуждение денежных поощрений для поддержки одаренных детей в области физической культуры и спорта Заявка на участие в конкурсе на присуждение денежных поощрений для поддержки одаренных детей в области физической культуры и спорта
1. Заявитель______________________________________________________________ 2. Фамилия, имя, отчество претендента на получение денежного поощрения_____________________________________________________ 3. Дата рождения ____________________ 4. Место учебы ____________________________________________________________ 5. Адрес __________________________________________________________________ 6. Контактные телефоны: заявителя ___________________________________, 7. претендента __________________________________________________________ 8. Образование ___________________________________________________________ 9. Основные спортивные достижения за учебный год
Операционное исчисление и некоторые его приложения. Математика-13: Учеб. пособ. / М.А. Евдокимов, Л.Г. Волкова; Самар. гос. техн. ун-т. Самара, 2007. 108 с. Продолжает серию учебников по высшей математике, издаваемых на кафедре высшей математики и прикладной информатики. Предназначено для студентов, которые изучают раздел математики, посвященный операционному исчислению, и преподавателей, ведущих занятия по данной теме. ISBN
Ил. 33. Библиогр.: 8 назв.
Печатается по решению редакционно-издательского совета Самарского государственного технического университета
Рецензент д-р техн. наук Э.Я. Раппопорт
ISBN ВВЕДЕНИЕ
В Например,
Символическое исчисление оказалось довольно удобным для решения различных задач, связанных с линейными дифференциальными уравнениями. Его популяризации в Обоснование символичного или, как стали называть, операционного метода было дано лишь в двадцатых годах двадцатого столетия Бромвичем и Карсоном, связавшими этот метод с известным из теории функций комплексного переменного методом интегральных преобразований, которым с успехом пользовались Коши, Лаплас и другие математики. При этом символ (оператор) Операционный метод получил также иное строгое обоснование с помощью общей теории операторов, развитый в функциональном анализе, представленной в работах В.А.Диткина и А.П.Прудникова. В последнее время весьма оригинальную и простую трактовку операционного метода дал польский математик Ян Микусинский. В данной работе излагаются основные положения операционного метода и особое внимание уделяется применению его для решения различных задач.
|

 веке многие математики (в том числе у нас в России, например, М.Е.Ващенко - Захарченко и А.В.Летников) занимались так называемым символическим исчислением. В основе этого исчисления лежало построение математического анализа как системы формальных операций над символом
веке многие математики (в том числе у нас в России, например, М.Е.Ващенко - Захарченко и А.В.Летников) занимались так называемым символическим исчислением. В основе этого исчисления лежало построение математического анализа как системы формальных операций над символом 
 (
( -независимая переменная).
-независимая переменная). - ная производная функции
- ная производная функции 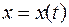 представляется как результат действия на
представляется как результат действия на  символа
символа 
 , левая часть линейного дифференциального уравнения с постоянными коэффициентами
, левая часть линейного дифференциального уравнения с постоянными коэффициентами - как результат действия на
- как результат действия на  символа.
символа. .
. веке в сильной мере способствовал английский инженер-электрик О.Хевисайд, который успешно использовал символическое исчисление в электротехнических расчетах.
веке в сильной мере способствовал английский инженер-электрик О.Хевисайд, который успешно использовал символическое исчисление в электротехнических расчетах. получил новое толкование, как комплексная переменная
получил новое толкование, как комплексная переменная  , а вместе с ним новую трактовку получил и сам операционный метод.
, а вместе с ним новую трактовку получил и сам операционный метод.


