ПРИМЕРЫ НАХОЖДЕНИЯ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ТАБЛИЦ 1 И 2
1).Найти изображение для оригинала Решение. 2).Найти изображение для оригинала Решение. 3).Найти изображение для оригинала Решение. 4).Найти изображение для оригинала Решение. Так как
5).Найти изображение для оригинала Решение. Так как
6).Найти изображение для оригинала Решение. Учитывая, что
7).Найти изображение для оригинала Решение. Так как
но если бы
8).Найти изображение для оригинала Решение. Так как по умолчанию
9).Найти изображение для оригинала Решение. По теореме запаздывания будем иметь:
10) Найти изображение для оригинала Решение. Применяя теоремы запаздывания и смещения, получим
11) Найти изображение для оригинала Решение. Применяя теорему дифференцирования изображения:
12)Найти изображение для оригинала Решение. Применяя теорему смещения:
13)Найти изображение для оригинала Решение. Применяя теорему интегрирования изображения:
14)Найти изображение для оригинала Решение. На основе свойства интегрирования оригинала:
Тогда
|

 .
. .
. .
.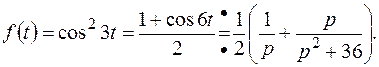
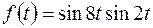

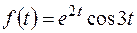 .
. (теорема смещения), то
(теорема смещения), то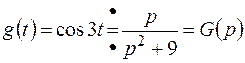 и
и .
. .
.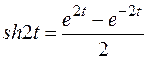 , то
, то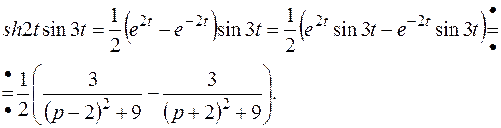
 .
. получаем:
получаем: .
.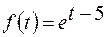 .
. , то
, то ;
; , то по теореме запаздывания:
, то по теореме запаздывания: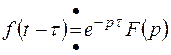 , получили бы
, получили бы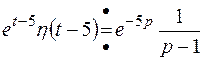 .
. .
. , то преобразуем
, то преобразуем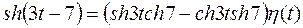 , тогда.
, тогда. .
. .
.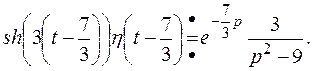
 .
.
 .
. имеем в данном случае:
имеем в данном случае: потому
потому
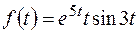 .
. и используя результат примера 11, получим
и используя результат примера 11, получим
 .
.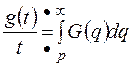 , имеем в данном случае:
, имеем в данном случае: тогда
тогда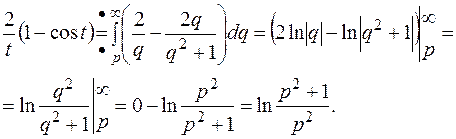
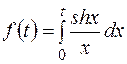 .
.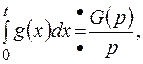 имеем в данном случае:
имеем в данном случае: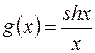 . Для нахождения
. Для нахождения  применим теорему интегрирования изображения:
применим теорему интегрирования изображения: в данном примере
в данном примере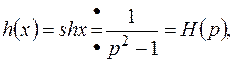 поэтому
поэтому




