Решение дифференциальных уравнений с переменными коэффициентами.
С помощью преобразования Лапласа можно выполнить интегрирование некоторых видов линейных дифференциальных уравнений с переменными коэффициентами. Пусть задано дифференциальное уравнение:
Рассмотрим случай, когда коэффициенты этого уравнения
………………………………………………………. Подставляя в уравнение полученные результаты, можно убедиться, что исходное дифференциальное уравнение преобразуется в дифференциальное уравнение относительно Целесообразность преобразования по Лапласу в том, что преобразованное дифференциальное уравнение оказывается более простым, чем исходное. Пример. Найти общее решение дифференциального уравнения
или
Получим линейное дифференциальное уравнение 1 порядка. Решим его методом Бернулли с помощью подстановки X=UV. При этом уравнение примет вид:
Согласно методу Бернулли будем иметь:
Тогда изображения искомого решения примет вид:
Возвращаясь к оригиналу, получим
8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами. Пусть дана система n дифференциальных уравнений 2го порядка.
где
Пусть заданы начальные условия
Пусть
Применяя к обеим частям каждого уравнения преобразование Лапласа, получим систему:
Эта алгебраическая система относительно неизвестных Пример. Решить систему
При начальных условиях x(0)=1, y(0)=0, z(0)=-1. Решение: Пусть В области изображений система примет вид:
Решим систему:
Аналогично найдутся и другие функции y (t) и z (t). Для решения системы дифференциальных уравнений операторным методом требуется решить только одну систему линейных алгебраических уравнений. При этом учитываются и начальные условия. Следует отметить возможность нахождения каждой неизвестной функции независимо от других. Проделать тоже самое классическим методом весьма затруднительно. 8.5 Линейные дифференциальные уравнения с запаздывающим аргументом. В ряде технических задач приходится иметь дело с дифференциальными уравнениями, в которых неизвестная функция входит при различных значениях аргумента, например:
и т.п. Такие уравнения называются дифференциальными уравнениями с отклоняющимися аргументами. Если Если Пусть дано дифференциальное уравнение с запаздывающим аргументом с постоянными коэффициентами
где Возьмем для простоты нулевые начальные условия
Применяя преобразования Лапласа, получим
Откуда найдем
от изображения переходим к оригиналу x(t). Пример: Решить уравнение.
Решение: В области изображений
8.6 Интегральные уравнения типа «свертки». Интегральным уравнением называется уравнение, содержащее искомую функцию под знаком интеграла. Например, -это линейное интегральное уравнение Фредгольма второго рода. Здесь y(x) – неизвестная функция, f(x) и r(x,t) – заданные функции. Функцию r(x,t) называют ядром уравнения (8.10), a и b=const. Изменим (8.10) следующим образом.
Получим линейное интегральное уравнение Вольтерра 2го рода. Если в (8.10) и (8.11) Если искомая функция y(x) входит только под знак интеграла, то (8.10) и (8.11) преобразуются в уравнения Фредгольма и Вольтерра 1го рода.
Совершенно очевидно, что большую роль в решении будет играть ядро уравнения, т.е. функция r(x,t). Важный класс уравнений Вольтерра получается, если ядро r(x,t) зависит только от разности r(x,t)=r(x-t). Уравнение в этом случае имеет вид.
Его еще называют уравнением типа свертки. Пусть входящие в уравнение (8.12) функции удовлетворяют условиям оригинала, тогда может быть найдено изображение функций по Лапласу
Пользуясь формулой свертки, получим операторное уравнение
Откуда
Для Ф(р) находим Пример. Решить интегральное уравнение
Решение:
Так же решаются и системы интегральных уравнений. Пример. Решить систему интегральных уравнений
|


 являются полиномами от t, тогда это уравнение может быть преобразовано по Лапласу, если воспользоваться теоремой дифференцирования изображения.
являются полиномами от t, тогда это уравнение может быть преобразовано по Лапласу, если воспользоваться теоремой дифференцирования изображения.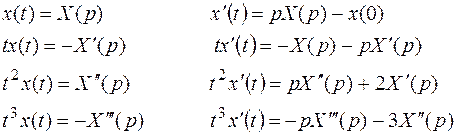
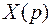 , но это уже будет обыкновенное линейное дифференциальное уравнение. Порядок этого уравнения будет такой, какова наивысшая степень t имеющаяся в исходном уравнении.
, но это уже будет обыкновенное линейное дифференциальное уравнение. Порядок этого уравнения будет такой, какова наивысшая степень t имеющаяся в исходном уравнении.

 .
.





 , (8.9)
, (8.9)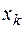 – к -тая функция, которую необходимо найти,
– к -тая функция, которую необходимо найти, - коэффициенты системы,
- коэффициенты системы, - правые части.
- правые части.



 ,
,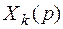 . Решим её и затем переходим к оригиналам.
. Решим её и затем переходим к оригиналам.
 ,
, 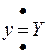 ,
, 
 или
или 


 .
.



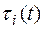 постоянные, то мы имеем так называемое дифференциально – разностное уравнение.
постоянные, то мы имеем так называемое дифференциально – разностное уравнение.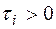 и старшая производная входит в дифференциально-разностноеуравнение только при одном значении аргумента, не меньшем всех других аргументов функций и производных, входящих в уравнение, то уравнение называют дифференциальным уравнением с запаздывающим аргументом.
и старшая производная входит в дифференциально-разностноеуравнение только при одном значении аргумента, не меньшем всех других аргументов функций и производных, входящих в уравнение, то уравнение называют дифференциальным уравнением с запаздывающим аргументом. ,
, = const,
= const,  .
. .
. .
.
 .
. откуда
откуда Переходим к оригиналу
Переходим к оригиналу .
.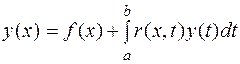 (8.10)
(8.10) (8.11)
(8.11) , то уравнения будут называться однородными.
, то уравнения будут называться однородными.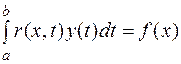 или
или  .
. (8.12)
(8.12)


 .
. .
. - решение интегрального уравнения (8.12).
- решение интегрального уравнения (8.12). .
.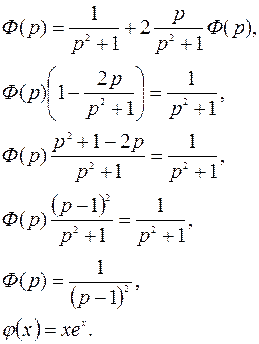
 в области изображений получим:
в области изображений получим: преобразовав, будем иметь:
преобразовав, будем иметь: или,
или, решим методом Крамера:
решим методом Крамера: