РЕШЕНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ И ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Методы операционного исчисления, основанные на идее использования преобразования Лапласа являются наиболее эффективным при решении основных задач для дифференциальных уравнений в частных производных. Неизвестная функция В первом случае преобразование Лапласа применяют к дифференциальному уравнению в частных производных по одной из двух независимых переменных в предположении, что другая остается неизменной. Полученное обыкновенное дифференциальное уравнение относительно изображения искомой функции интегрируется не операционным методом, а классическим. Возвращаясь от полученного изображения к оригиналу, находим решение поставленной задачи. Во втором случае к обыкновенному дифференциальному уравнению относительно изображения искомой функции опять применяют преобразование Лапласа, но по другой независимой переменной. В результате получают алгебраическое уравнение, из которого находят «двукратное» изображение искомой функции. С помощью двух обратных преобразований Лапласа восстанавливается искомая функция Решение дифференциального уравнения, найденное с помощью двукратного преобразования Лапласа, не зависит от того, в какой последовательности применялись прямые и обратные преобразования. Удачно выбранный порядок в двукратном преобразовании может значительно облегчить решение задачи. Операционный метод удобнее применять при решении задач математической физики, если: начальные условия нулевые; существуют изображения для всех функций, входящих в уравнение; изображение искомого решения удовлетворяет следующим условиям:
Пример 1 Найти решение уравнения
Применим преобразование Лапласа по переменной
Заданное уравнение примет вид:
и решим методом Бернулли. Согласно этому методу,
Осуществляя данную подстановку в уравнение, получим
Решая первое уравнение системы, получим
Подставим найденную функцию W во второе уравнение, будем иметь:
Откуда
Тогда
Так как
Возвращаясь к оригиналу, получим
Пример 2. Найти решение уравнения Сначала применим преобразование Лапласа по переменной
Условие Применим преобразование Лапласа еще раз, но уже по переменной
Это алгебраическое уравнение относительно «двукратного» изображения - Решим его:
Возвращаясь к оригиналу по p, получаем:
Возвращаясь к оригиналу по q, получаем:
Пример 3. Найти формулу колеблющейся струны, закрепленной на концах, если начальные скорости ее точек равны нулю, а начальные отклонения заданы соотношением Подстановка задачи: найти решение уравнения
Будем решать эту задачу методом Лапласа. Применим преобразование Лапласа по переменной t, предварительно переписав уравнение в виде
Будем иметь
Граничные условия при этом примут вид:
Относительно изображения искомого решения – функции
где
Составим и решим характеристическое уравнение
Тогда общее решение однородного уравнения примет вид
Для нахождения B и C вычислим:
и подставим в уравнение:
Тогда
Для нахождения С1 и С2 удовлетворим граничным условиям:
Очевидно, что С1= С2=0. Таким образом, имеем Возвращаясь к оригиналу, получим:
Пример 4. Найти решение уравнения теплопроводности Применяя к уравнению теплопроводности преобразование Лапласа по переменной t, получим:
Граничные условия при этом примут вид:
Перепишем полученное обыкновенное дифференциальное уравнение в виде:
Его общее решение: где
Составим и решим характеристическое уравнение:
Тогда
Второе слагаемое
Оно имеет вид Тогда
Подставляя в уравнение, находим:
Отсюда
Тогда
Удовлетворим граничным условиям:
При этом
Возвращаясь к оригиналу, получим:
|

 , удовлетворяющая дифференциальному уравнению в частных производных и заданным условиям, может быть определена с помощью однократноголибо двукратногопреобразования Лапласа.
, удовлетворяющая дифференциальному уравнению в частных производных и заданным условиям, может быть определена с помощью однократноголибо двукратногопреобразования Лапласа.



 , если
, если 


 , тогда
, тогда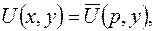





 или
или
 или
или


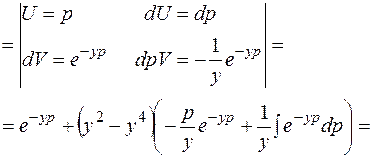


 - изображение по Лапласу, то
- изображение по Лапласу, то  и тогда принимаем С=0, то есть
и тогда принимаем С=0, то есть 

 , удовлетворяющее условиям
, удовлетворяющее условиям  ,
, 


 , получим
, получим






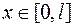 ,
,  , неравное тождественно нулю, удовлетворяющее граничным условиям:
, неравное тождественно нулю, удовлетворяющее граничным условиям:





 получим обыкновенное дифференциальное уравнение второго порядка, неоднородное, с правой частью специального вида. Его решение
получим обыкновенное дифференциальное уравнение второго порядка, неоднородное, с правой частью специального вида. Его решение
 - общее решение однородного уравнения
- общее решение однородного уравнения


 - частное решение неоднородного уравнения. Его вид с точностью до неопределенных коэффициентов будет
- частное решение неоднородного уравнения. Его вид с точностью до неопределенных коэффициентов будет


 Отсюда имеем:
Отсюда имеем:





 , удовлетворяющие начальному условию
, удовлетворяющие начальному условию  , где
, где  и граничным условиям
и граничным условиям  и
и  .
.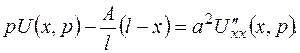






 .
.








 или
или 



