Решение линейных дифференциальных уравнений с постоянными коэффициентами.
Возьмем неоднородное линейное дифференциальное уравнение второго порядка
и найдем его частное решение при начальных условиях
Считаем исходную функцию x(t) и правую часть f(t) оригиналами и переходим от уравнения (8.1) связывающего оригиналы к уравнению, связывающему изображения X(p) и F(p).
Изображение уравнения (8.1) будет:
Мы получили уже не дифференциальное, а алгебраическое уравнение относительно X(p).
Откуда получим операторное решение д.у.
Найдено изображение искомого решения. Теперь по таблицам или формулам обращения найдем x(t). Если начальные условия нулевые, то операторное решение будет иметь простой вид:
Пример. Найти решение уравнения
при нулевых начальных условиях. Решение: x(t)=X(p):
1) 2) 3) Тогда Изложенный метод применим к решению линейного дифференциального уравнения любого порядка. Пример.
Решение. Составим операторное уравнение.
Здесь полюса 3х кратные комплексно – сопряженные. Поэтому найдем только вычет в точке i.
Взяв, удвоенную действительную часть полученного выражения, находим
Покажем, как следует поступать, если начальные условия заданы не в нулевой точке. Пример. Решить уравнение х(1)=1 х/(1)=0. Решение: введем новую переменную x(t)=x( Теперь уравнение и начальные условия перепишутся в виде:
Пусть
В некоторых случаях правая часть задается в виде комбинации различных аналитических выражений взятых на различных интервалах, или даже графически. Если эта функция является оригиналом, то можно применить операторный метод решения. Пример. Решить задачу Коши.
если f(t) задана графически (рис.8.1).
Решение: Запишем
Применяя теорему запаздывания, получим
Пусть x(t)=X(p), получим операторное уравнение.
Откуда,
Так как Применяя теперь теорему запаздывания, получим
или
|

 (8.1)
(8.1)

 .
. .
. .
.

 .
.


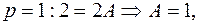



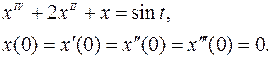

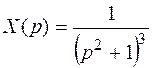 .
.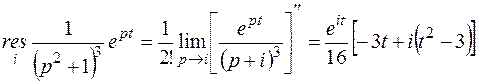

 , при начальных условиях
, при начальных условиях , положив t=
, положив t=  .
. .
.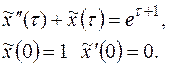




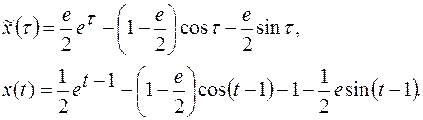


 в аналитическом виде с помощью функции
в аналитическом виде с помощью функции  :
:
 .
. .
.
 .
.
 .
.


