С) Интегрирование оригинала.Если
Т.е. интегрирование оригинала в пределах от 0 до t приводит к делению изображения на р. Доказательство: Заметим, что Пусть Найдем изображение производной
В то же время
Приравнивая правые части, получим
т.е.
Важнейшее свойство преобразования Лапласа- это то, что сложным действиям дифференцирования и интегрирования в пространстве оригиналов соответствуют простые алгебраические действия умножения и деления на р в пространстве изображений.
9с) Дифференцирование изображений.
т.о. дифференцирование изображения сводится к умножению оригинала на (–t). Доказательство:
Справа стоит интеграл Лапласа для функции
Применяя теорему n раз получим
Пример. Найти изображение степенной функции Если
Повторяем умножение – дифференцирование.
По индукции нетрудно получить формулу
С помощью Г функции формулу можно распространить на любые
С) Интегрирование изображений. Если
Интегрирование изображения в пределах от р до Доказательство:
Этот интеграл – есть изображение по Лапласу функции Пример. Найти изображение функции Решение:
|
и 
, то 
.
, 
.
.
.
,
.
,
.
,т.е.
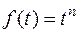, используя 9с).
, то получить формулу можно последовательным дифференцированием и умножением на – t.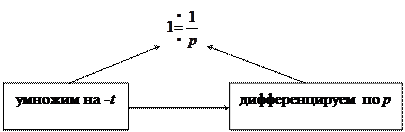
.
.
.
.
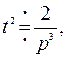
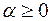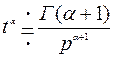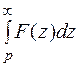сходится, то
.
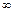соответствует делению оригинала на t.
.
.
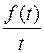, тогда
