Конечные разности решетчатых функций.
Выражение
называется конечной разностью первого порядка решетчатой функции, или просто первой разностью. Ясно, что
Разность к – го порядка решетчатой функции
Разность любого порядка можно выразить через значения решетчатой функции
Аналогично для третьей разности:
Для разности произвольного порядка к справедлива формула
где
Пример.
Формулы (11.1)-(11.6) позволяют выразить саму решетчатую функцию Из (11.1)
Из (11.2)
откуда
Используя равенство (11.3) при к=3 и равенства (11.4), (11.7), (11.8) получим
Продолжая вычисления можно получить общую формулу
при n=0
Формулы (11.10) и (11.11) выражают значения решетчатой функции через её конечные разности до порядка l включительно. Эти формулы являются дискретным аналогом разложения непрерывных функций в ряд Тейлора. Примеры. 1).
2).
3).
4).
Отметим, что операция взятия конечных разностей является линейной операцией, что следует из определения конечной разности
Используя выражение (11.1), можно вывести формулу для вычисления разности произведений 2-х функций
|
(11.1)
- представляет собой решетчатую функцию, для которой может быть вычислена конечная разность. Т.о. первая разность от решетчатой функции 
называется разностью второго порядка решетчатой функции 
, или просто второй разностью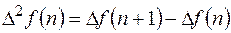
(11.2)
определяется формулой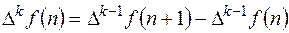
(11.3)
.
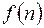(11.4)
(11.5)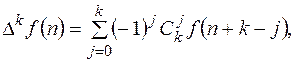
(11.6)
. так называемые биноминальные коэффициенты, такие что: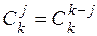
.
(11.7)
. (11.8)
(11.9)
, (11.10)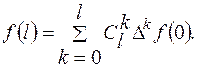
(11.11)
,
.
.
.
.
