С) Теорема линейности.
Линейность D – преобразования.
С) Смещение в области оригиналов. Если
и С) Теорема затухания. Смещение в области изображений. Если
Эти свойства доказываются непосредственным применением формулы D – преобразования. С) Теорема о разности решетчатой функции. Изображение конечных разностей. Если
Доказательство:
ч.т.д. Если функция Многократно применяя предыдущую формулу нетрудно получить
Последняя формула значительно упрощается, если решетчатая функция обращается в ноль при n= 0,1,…, к-1:
С) Теорема о сумме решетчатой функции. Изображение конечной суммы. Если
Пусть
С) Дифференцирование изображений. Если
Доказать можно дифференцированием ряда выражающего D – преобразование.
С) Интегрирование изображений. Если
С) Умножение изображений. Определим свертку решетчатых функций
Если Произведению изображений соответствует свертка оригиналов.
|
, то
.
.
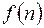допускает D – преобразование, то её разность произвольного порядка к также допускает D – преобразование, поскольку разность 
представима в виде линейной комбинированной решетчатой функции 
.
,…
.
.
, то
.
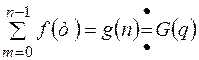, т.к. 
, то применяя теорему о разности 
т.о.
.
,
и 
, то существует интеграл от изображения 
, определяемый равенством
.
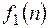и 
как решетчатую функцию, определяемую формулой
, то 
.
