ПРИМЕНЕНИЕ ОПЕРАТОРНЫХ МЕТОДОВ ДЛЯ АНАЛИЗА ЛИНЕЙНЫХ СИСТЕМ
При анализе и синтезе систем автоматического управления и регулирования устройств связи широкое распространение получили следующие основные методы математического исследования: операторный метод, метод интеграла свертки (временный метод) и частотный метод. Эти методы, как и классический, основанный на теории дифференциальных уравнений, играют важнейшую роль в теории линейных систем. Все они связаны друг с другом, но каждый из них имеет свои особенности, которые оказываются более приспособленными для решения специфических задач, встречающихся в технике. 1). Передаточная функция системы. Линейными системами в теории электрических цепей, автоматического регулирования и управления называют системы, функционирование которых во времени описывается линейными дифференциальными уравнениями (рис.10.1). Обозначим: f(t) – входное воздействие на систему (входной сигнал); x(t) – реакция (отклик) системы на входное воздействие (выходной сигнал);
А – оператор линейной системы: x(t)= А [ f(t) ], А: А [ λ1 f1(t)+ λ2 f2(t) ] = λ1 А [ f1(t) ] + λ2 А [ f2(t) ]. Выход и вход линейной системы связаны линейным дифференциальным уравнением:
где
( Многочлен Перейдем к решению задачи о связи выходного и входного сигналов системы в плоскости комплексной переменной
где
Обратный переход во временную область действительной переменной t осуществляется с помощью обратного преобразования Лапласа
Как известно, операторы Перейдем к изображениям членов дифференциального уравнения (10.1) при нулевых начальных условиях:
Получим
Где -характеристический многочлен, соответствующий символическому многочлену (10.2) в плоскости изображений. Обозначим:
Функция Положим Учитывая, что
Таким образом, для нахождения передаточной функции системы
Из уравнения (10.5) оригинал
( При практическом применении операторных методов исследования линейных систем передаточная функция Формула (10.6) позволяет исследовать анализируемую реальную систему на адекватность выбранной математической модели. Для этого нужно определить из эксперимента реакцию системы на импульсное воздействие и сравнить с
2).Характеристики элементов электрических цепей в операторной форме. Рассмотрим электрическую цепь, содержащую активное сопротивление, катушку индуктивности и конденсатор (реактивные элементы) (рис.10.2).

Найдем передаточные функции этих элементов.
2.1. Активное сопротивление. По закону Ома
Переходя к изображениям, получим
2.2. Индуктивное сопротивление. Обозначим L – индуктивность катушки. Из электротехники известно:
Переходя к изображениям (при
Можно интерпретировать (в математическом отношении) 2.3. Емкостное сопротивление. Из электротехники известно:
Полагая Как и в предыдущем случае, можно говорить о сопротивлении конденсатора в операторной форме
Преобразование Лапласа является линейным. Поэтому известные в электротехнике законы Кирхгофа имеют свои аналоги в плоскости изображений: 1) 2) Использование этих законов позволяет находить общее сопротивление электрической цепи при последовательном и параллельном соединении активных и реактивных элементов по правилам, принятым для расчетов сопротивлений соответствующих соединений активных сопротивлений. 3) Примеры нахождения передаточных функций электрических цепей. 3.1. Дифференцирующее звено (рис. 10.3).

Произведение
Если
Переходя к оригиналам, получим
Поэтому рассматриваемую цепь называют дифференцирующим звеном. Для оценки качества (по различным критериям) электрических, электромеханических систем, систем автоматического управления и регулирования переходя к изображениям, получим проводят исследование (как теоретическое, так и экспериментальное) реакции системы на единичное входное воздействие («скачок»).
Поэтому из (10.5)
где
Для исследуемой цепи
Переходя к оригиналу (используя таблицу изображений), получим
График переходной функции изображен на рис.10.4.
3.2. Интегрирующее звено (рис 10.5).
В операторной форме
Звено с такой передаточной функцией называют апериодическим звеном первого порядка. Если
Переходя к оригиналам, получим
Поэтому такое звено называют интегрирующим.
Для определения переходной функции
График переходной функции изображен на рис.10.6.
3.3. Колебательное звено (рис.10.7).
В операторной форме
Величина LC имеет размерность (сек2). Обозначив
Найдем переходную функцию
Для нахождения 1) 2) разложение правильной дроби на простейшие:
Коэффициенты А, В, С найдем методом неопределенных коэффициентов:
3)
Замечание. При Если
Используя таблицу изображений, найдем оригинал:
График переходной функции приведен на рис.10.9
Обозначив
Звено с такой передаточной функцией называют апериодическим звеном второго порядка. Это звено эквивалентно двум последовательно соединенным апериодическим звеньям с одинаковыми постоянными времени. При
где При единичном входном возмущении
Переходя к оригиналу, получим
где Рассматриваемое звено, как и в предыдущем случае, называют апериодическим звеном второго порядка, которое эквивалентно двум последовательно соединенным апериодическим звеньям первого порядка с различными постоянными времени График переходной функции
4). Частотные характеристики линейных систем. Общее решение уравнения (10.1) имеет вид:
Где
Оператору
Если все корни характеристического уравнения имеют отрицательные действительные части ( Пусть Будем искать частное решение в виде
Подставив
Функция
Найдем частотные характеристики электрических цепей, рассмотренных в 3.1, 3.2, 3.3. 4.1. Дифференцирующее звено.
График амплитудно-частотной характеристики приведен на рис.10.11.
Низкие частоты подавляются (коэффициент усиления уменьшается при уменьшении
4.2. Интегрирующее звено.
Устройство называют фильтром низких частот (высокие частоты подавляются).
4.3. Колебательное звено.
Нетрудно показать, что на этой частоте
На рис. 10.13 приведена амплитудно-частотная характеристика колебательного звена.
Рис. 10.13
При малых потерях в колебательном контуре (R – малая величина) величина Для исследования процессов в колебательном звене при резонансе частотный метод использовать нельзя, т.к. он не отражает переходных процессов и пригоден лишь для исследования установившихся режимов. Поэтому воспользуемся операторным методом исследования, положив
передаточная функция колебательного звена при отсутствии потерь. Частоту
Используя таблицу изображений, найдем
Слагаемое
Эффект резонанса широко используется, например, в радиотехнических устройствах при выделении полезного сигнала заданной частоты из всего спектра сигналов, поступающих в приемное устройство. В механических системах явление резонанса может быть использовано при создании вибрационных машин (амплитуда колебаний вибратора должна быть максимально большой). В качестве отрицательного результата явления резонанса можно рассматривать разрушение механических конструкций при совпадении собственной частоты их колебаний и частоты внешнего возмущающего воздействия.
4.4. Фазоопережающее звено. Фазоопережающие звенья используются для достижения устойчивости систем автоматического регулирования и коррекции их динамических характеристик. Поэтому такие звенья называют корректирующими. Практически корректирующие звенья часто реализуются на операционных усилителях, включая необходимые активные и реактивные элементы на выходе усилителя или в обратную связь. На рис.10.14 приведена простейшая схема фазоопережающего звена.

Передаточная функция устройства находится по формуле
В рассматриваемой цепи
Рассматриваемое корректирующее устройство имеет передаточную функцию
где k – коэффициент усиления звена на нулевой частоте;
В качестве примера рассмотрим корректирующее фазоопережающее звено с параметрами:
График АЧХ представлен на рис. 10.15.
График ФЧХ представлен на рис. 10.16.
Из графиков следует, что коэффициент усиления звена при
|

 t – время.
t – время. , (10.1)
, (10.1) – символический многочлен:
– символический многочлен: , (10.2)
, (10.2) ).
).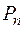 называют оператором линейного дифференциального уравнения.
называют оператором линейного дифференциального уравнения. . Такой переход осуществляется путем преобразования Лапласа
. Такой переход осуществляется путем преобразования Лапласа ,
, - функция-оригинал,
- функция-оригинал, 
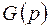 - изображение
- изображение  - оператор преобразования Лапласа.
- оператор преобразования Лапласа. ,
, - оператор обратного преобразования Лапласа (на месте
- оператор обратного преобразования Лапласа (на месте 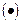 записывается преобразуемая функция).
записывается преобразуемая функция). и
и  являются линейными операторами.
являются линейными операторами.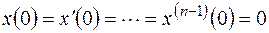 .
. , (10.3)
, (10.3) (10.4)
(10.4)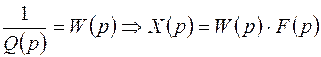 , где (10.5)
, где (10.5) - изображение входного воздействия на систему;
- изображение входного воздействия на систему; - изображение реакции системы на входное воздействие.
- изображение реакции системы на входное воздействие.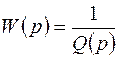 называется передаточной функцией системы. Эта функция отражает внутреннюю структуру исследуемой системы. Она играет роль оператора А в плоскости изображений.
называется передаточной функцией системы. Эта функция отражает внутреннюю структуру исследуемой системы. Она играет роль оператора А в плоскости изображений. , где
, где  - импульсная функция Дирака.
- импульсная функция Дирака. , получим
, получим . (10.6)
. (10.6)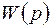 достаточно получить отклик
достаточно получить отклик 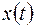 системы на импульсное воздействие
системы на импульсное воздействие  .
.
 (10.7)
(10.7)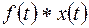 - свертка функций
- свертка функций  и
и 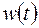 ).
). .
. ,
,  .
. - напряжение на катушке индуктивности.
- напряжение на катушке индуктивности. ), получим:
), получим: .
.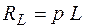 как индуктивное сопротивление элемента L в операторной форме в плоскости изображений.
как индуктивное сопротивление элемента L в операторной форме в плоскости изображений. - напряжение на конденсаторе емкостью С.
- напряжение на конденсаторе емкостью С. и
и  .
. .
. - 1-ый закон Кирхгофа (сумма изображений токов в узле равна нулю);
- 1-ый закон Кирхгофа (сумма изображений токов в узле равна нулю); - 2-ой закон Кирхгофа (сумма изображений падений напряжения на элементах электрической цепи в замкнутом контуре, не содержащем источников э.д.с. (электродвижущей силы) равна нулю).
- 2-ой закон Кирхгофа (сумма изображений падений напряжения на элементах электрической цепи в замкнутом контуре, не содержащем источников э.д.с. (электродвижущей силы) равна нулю). ;
;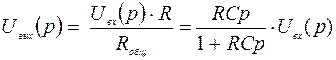 .
. имеет размерность времени (сек). Величину
имеет размерность времени (сек). Величину  называют постоянной времени
называют постоянной времени  . (10.8)
. (10.8)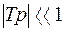 (физически это означает, что
(физически это означает, что  , где
, где  наибольшая частота в спектре входного воздействия), то
наибольшая частота в спектре входного воздействия), то ;
;  .
. .
. ,
,  .
. при единичном входном воздействии называют переходной функцией и обозначают через
при единичном входном воздействии называют переходной функцией и обозначают через  . Знание переходной функции
. Знание переходной функции  системы при любом входном воздействии
системы при любом входном воздействии  . Действительно, если
. Действительно, если  , то
, то
 ,
,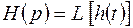 . При произвольном входном воздействии
. При произвольном входном воздействии  По формуле Дюамеля
По формуле Дюамеля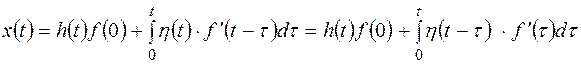 .
.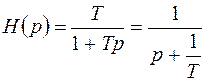 .
.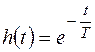 .
.

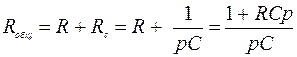 ,
, ,
, . (10.9)
. (10.9) (физически это означает, что
(физически это означает, что  , где
, где 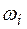 наименьшая частота в спектре входного воздействия), то
наименьшая частота в спектре входного воздействия), то .
. .
. ,
,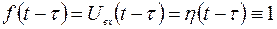 ,
,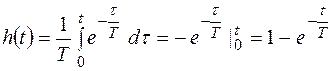 .
.

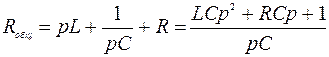 ,
,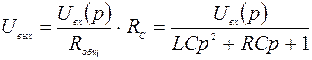 ,
, .
.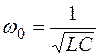 ,
, 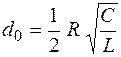 , приведем передаточную функциюколебательного звена к стандартному виду:
, приведем передаточную функциюколебательного звена к стандартному виду: . (10.10)
. (10.10) . (10.11)
. (10.11) - выделение полного квадрата в знаменателе; рассмотрим случай
- выделение полного квадрата в знаменателе; рассмотрим случай  (при этом квадратному трехчлену в знаменателе соответствует пара комплексно-сопряженных корней);
(при этом квадратному трехчлену в знаменателе соответствует пара комплексно-сопряженных корней); ;
; ,
, 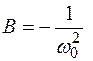 ,
,  .
.
 Подставив полученное выражение в (10.11) и переходя к оригиналам (используем таблицу изображений по Лапласу), получим
Подставив полученное выражение в (10.11) и переходя к оригиналам (используем таблицу изображений по Лапласу), получим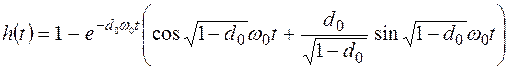
 График переходной функции
График переходной функции  колебательного звена приведен на рис.10.8.
колебательного звена приведен на рис.10.8.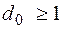 корни знаменателя в
корни знаменателя в 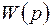 действительные отрицательные, поэтому
действительные отрицательные, поэтому  или
или  и колебательность в
и колебательность в  , то
, то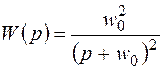 , и
, и
 .
.
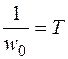 , передаточную функцию можно представить в виде
, передаточную функцию можно представить в виде .
.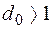 оба корня знаменателя передаточной функции будут вещественными и отрицательными. Поэтому,
оба корня знаменателя передаточной функции будут вещественными и отрицательными. Поэтому,  ,
, ,
,  .
.
 ,
, .
. и
и 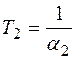 .
.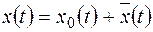
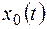 - общее решение соответствующего однородного уравнения;
- общее решение соответствующего однородного уравнения; - частное решение данного уравнения.
- частное решение данного уравнения. уравнения (10.1) соответствует характеристическое уравнение
уравнения (10.1) соответствует характеристическое уравнение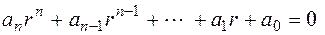 .
. ), то
), то  . Это обусловлено тем, что
. Это обусловлено тем, что  (для простого корня) или
(для простого корня) или  (для k – кратного корня), модули которых стремятся к 0 при
(для k – кратного корня), модули которых стремятся к 0 при  (
(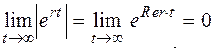 , т.к.
, т.к.  ). Функция
). Функция  - установившийся режим (колебания системы обусловлены входным воздействием
- установившийся режим (колебания системы обусловлены входным воздействием 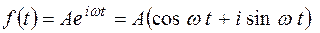 ,
,  ,
,  (множество комплексных чисел).
(множество комплексных чисел).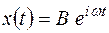 ,
,  - неизвестное число, подлежащее определению.
- неизвестное число, подлежащее определению. ;
;  и вообще,
и вообще, .
. .
. характеризует частотные свойства линейной системы. Нетрудно видеть, что
характеризует частотные свойства линейной системы. Нетрудно видеть, что  . Представим
. Представим  ,
, - амплитудно-частотная характеристика системы (коэффициент усиления системы на частоте
- амплитудно-частотная характеристика системы (коэффициент усиления системы на частоте  );
);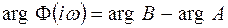 - фазочастотная характеристика системы (она выражает сдвиг по фазе выходного сигнала системы по отношению к входному сигналу на частоте
- фазочастотная характеристика системы (она выражает сдвиг по фазе выходного сигнала системы по отношению к входному сигналу на частоте  ;
;  ;
;  ;
; ;
;  .
.

 ;
;  .
. ;
;  ;
; 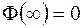 .
. График
График  приведен на рис 10.12.
приведен на рис 10.12. .
. ,
,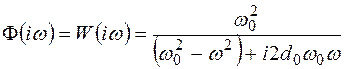 ,
, ,
, ,
, .
. называется резонансной частотой колебательного контура.
называется резонансной частотой колебательного контура. .
.

 мала и при частотах входного воздействия близких к
мала и при частотах входного воздействия близких к  наблюдается резкое увеличение амплитуды колебаний выходного напряжения (происходит «раскачка» системы). Это явление носит название резонанса.
наблюдается резкое увеличение амплитуды колебаний выходного напряжения (происходит «раскачка» системы). Это явление носит название резонанса. (физически это означает отсутствие потерь в колебательном звене, что имеет место при R = 0). Подобная идеализация реальных процессов позволяет выявить существенные моменты, имеющие место при резонансе.
(физически это означает отсутствие потерь в колебательном звене, что имеет место при R = 0). Подобная идеализация реальных процессов позволяет выявить существенные моменты, имеющие место при резонансе. -
-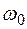 называют собственной частотой колебательного звена. Найдем выходной сигнал колебательного звена при
называют собственной частотой колебательного звена. Найдем выходной сигнал колебательного звена при  (амплитуду выходного сигнала можно принять равной 1).
(амплитуду выходного сигнала можно принять равной 1). ;
;

 .
. отражает как раз тот факт, который был назван «раскачкой системы»: при воздействии на систему с частотой равной резонансной, происходит увеличение амплитуды колебаний выходного сигнала.
отражает как раз тот факт, который был назван «раскачкой системы»: при воздействии на систему с частотой равной резонансной, происходит увеличение амплитуды колебаний выходного сигнала.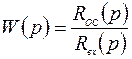 , где
, где - операторное сопротивление цепи обратной связи операционного усилителя (ОУ),
- операторное сопротивление цепи обратной связи операционного усилителя (ОУ),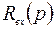 - операторное сопротивление входной цепи ОУ.
- операторное сопротивление входной цепи ОУ.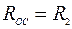 ;
;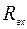 - операторное сопротивление параллельно соединенных конденсатора и резистора
- операторное сопротивление параллельно соединенных конденсатора и резистора  .
. , где
, где  .
. ,
,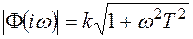 - амплитудно-частотная характеристика звена (АЧХ);
- амплитудно-частотная характеристика звена (АЧХ);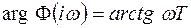 - фазочастотная характеристика звена (ФЧХ).
- фазочастотная характеристика звена (ФЧХ).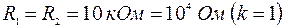 ,
,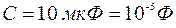 ,
, .
. - часть ветви гиперболы с полуосями a = 1, b = 10 (ось
- часть ветви гиперболы с полуосями a = 1, b = 10 (ось 
 .
.
 больше 1 и на любой частоте выходное напряжение опережает по фазе входное напряжение (поэтому звено и называют фазоопережающим).
больше 1 и на любой частоте выходное напряжение опережает по фазе входное напряжение (поэтому звено и называют фазоопережающим).


