Суммирование решетчатых функций.Рассмотрим теперь операцию, которая является обратной по отношению к операции взятия конечной разности. Пусть решетчатая функция Эта задача аналогична задаче о нахождении первообразной в анализе обычных функций. Искомая функция имеет вид
Действительно,
Функцию F (n) называют первообразной для решетчатой функции Если F (n) является первообразной для Если решетчатая функция
При этом условии первообразная определяется выражением
И общий вид первообразной для данной решетчатой функции
Значение постоянной С можно выразить через значение первообразной при некотором фиксированном значении аргумента n=N.
Откуда,
для любого n>N. Эта формула является аналогом формулы Ньютона – Лейбница, а выражение стоящее справа иногда называют определенной суммой. Эту формулу можно преобразовать:
Учитывая, что
при N=0 получим
Пример. Для
по формуле суммы членов геометрической прогрессии.
|
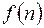определена при положительных значениях аргумента n=0,1,2… Требуется найти такую решетчатую функцию F(n), для которой функция 
.
, то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечном n сходился ряд
.
.
.
.
.
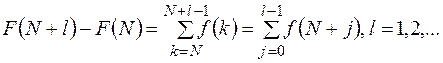
можно записать и так.
, а
.
найти сумму F (n).
