Преобразование обратное по отношению к дискретному преобразованию Лапласа определяет решетчатую функцию 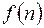 по заданному изображению
по заданному изображению  и определяется формулой
и определяется формулой
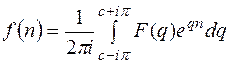 (11.14)
(11.14)
где С > 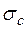 .
.
Вычисление оригиналов 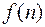 можно производить и по формуле обращения Z – преобразования, которая может быть получена из формулы (11.14) путем замены переменной
можно производить и по формуле обращения Z – преобразования, которая может быть получена из формулы (11.14) путем замены переменной 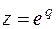 .
.
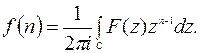 (11.15)
(11.15)
Интегрирование производится по окружности С радиуса 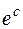 , где С>
, где С> 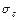 в положительном направлении. Функция, стоящая под интегралом
в положительном направлении. Функция, стоящая под интегралом 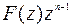 - аналитическая вне окружности С и на самой окружности. Применяя теорему о вычетах получим:
- аналитическая вне окружности С и на самой окружности. Применяя теорему о вычетах получим:
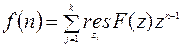 , (11.16)
, (11.16)
где  - полюс функции
- полюс функции 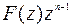 , лежащий внутри окружности С.
, лежащий внутри окружности С.
Иногда оказывается более удобным определять вычеты, не переходя к Z – преобразованию. Тогда формула (11.16) принимает вид
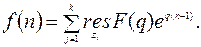 (11.17)
(11.17)
Пример.
Найти оригинал 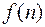 , соответствующий изображению
, соответствующий изображению
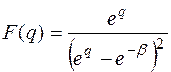 .
.
Решение. Выполним замену переменной
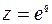 ,
, 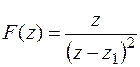 , где
, где  .
.
Образуем функцию
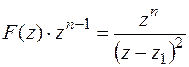 .
.
Находим вычет в точке 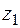 - это двукратный полюс
- это двукратный полюс
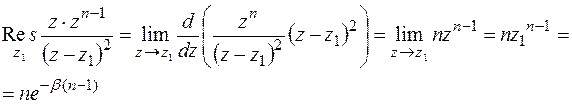
Таким образом,
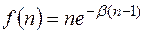 .
.
Свойства дискретного преобразования Лапласа.
Дискретное преобразование Лапласа устанавливает соответствие между решетчатыми функциями – оригиналами 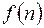 и их изображениями
и их изображениями  . Различным операциям, совершаемыми над решетчатыми функциями, соответствуют при этом определенные операции, совершаемые над их изображениями.
. Различным операциям, совершаемыми над решетчатыми функциями, соответствуют при этом определенные операции, совершаемые над их изображениями.

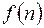 по заданному изображению
по заданному изображению  и определяется формулой
и определяется формулой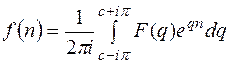 (11.14)
(11.14)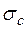 .
.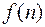 можно производить и по формуле обращения Z – преобразования, которая может быть получена из формулы (11.14) путем замены переменной
можно производить и по формуле обращения Z – преобразования, которая может быть получена из формулы (11.14) путем замены переменной 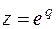 .
.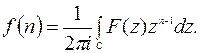 (11.15)
(11.15)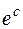 , где С>
, где С> 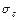 в положительном направлении. Функция, стоящая под интегралом
в положительном направлении. Функция, стоящая под интегралом 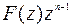 - аналитическая вне окружности С и на самой окружности. Применяя теорему о вычетах получим:
- аналитическая вне окружности С и на самой окружности. Применяя теорему о вычетах получим: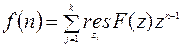 , (11.16)
, (11.16) - полюс функции
- полюс функции 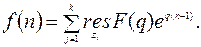 (11.17)
(11.17)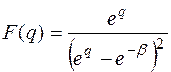 .
.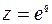 ,
, 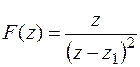 , где
, где  .
.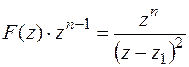 .
.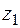 - это двукратный полюс
- это двукратный полюс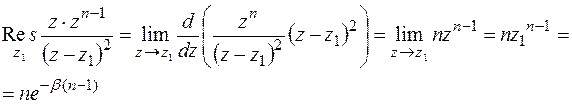
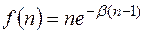 .
.


