Решение систем линейных алгебраических уравнений методом Гаусса. Пусть требуется решить систему уравнений
Пусть требуется решить систему уравнений
Исключая сначала
Таким образом осуществлен прямой ход в методе Гаусса. В процессе обратного хода последовательно исключаются
Пусть теперь дана система из n линейных уравнений с n неизвестными
… … … … …
Разделив первое уравнение на
где Умножим разрешающее уравнение (5) на Система примет вид
… … … …
где
Затем, оставляя без изменения первое уравнение, повторяем процедуру к оставшейся системе из n - 1 одного уравнения и т.д. В результате получаем
… … … …
Прямой ход выполнен. При выполнении обратного хода путем последовательного исключения неизвестных
В модифицированном методе Гаусса с выбором максимального элемента по столбцу в начале 1-го шага прямого хода среди коэффициентов В начале второго шага ищется максимальный по модулю элемент среди коэффициентов Модифицированный алгоритм Гаусса уменьшает погрешность вычислений. Блок-схема решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента (по столбцу) приведена на рис. 2.1
|


 (1)
(1) 
 из второго и третьего уравнений, а затем
из второго и третьего уравнений, а затем  из третьего уравнения, получаем
из третьего уравнения, получаем
 (2)
(2) .
. из второго и первого уравнений. В результате получаем решение системы уравнений (1)
из второго и первого уравнений. В результате получаем решение системы уравнений (1)
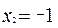
 (3)
(3)
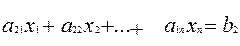 (4)
(4)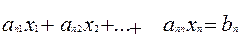
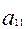 , получим разрешающее уравнение
, получим разрешающее уравнение , (5)
, (5) ,
, 
 и вычтем полученное уравнение из второго уравнения системы (4). Аналогично преобразуем остальные уравнения.
и вычтем полученное уравнение из второго уравнения системы (4). Аналогично преобразуем остальные уравнения.
 (6)
(6) ,
,

 j = 2,3,...,n
j = 2,3,...,n (7)
(7)
 и т.д. из системы (7), получаем решение задачи
и т.д. из системы (7), получаем решение задачи
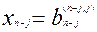

 (8)
(8) i = 1,2,...,n при неизвестном x находят наибольший по модулю. Пусть это
i = 1,2,...,n при неизвестном x находят наибольший по модулю. Пусть это  . После этого в исходной системе меняют местами 1-ое и J-ое уравнения. Далее выполняется описанный выше метод.
. После этого в исходной системе меняют местами 1-ое и J-ое уравнения. Далее выполняется описанный выше метод. i = 2,3,...,n. При необходимости вновь делают перестановку и т. д.
i = 2,3,...,n. При необходимости вновь делают перестановку и т. д.


