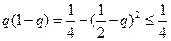Оценки погрешностей интерполяционных формул Ньютона
Если узлы интерполирования
Где (Для интерполирования При расчетах порядок n разностей выбирается таким, что можно положить:
При этом остаточные члены интерполяционных формул Ньютона будут равны
Пример: В пятизначных таблицах логарифмов даются логарифмы целых чисел от х=1000 до х=10000 с предельной абсолютной погрешностью, равной Решение: Т.к. Отсюда
Из формулы (1) при n=11 и h=1 получаем:
Т.к.
Окончательно получаем:
Т.о. погрешность интерполирования не превосходит погрешностей исходных данных! Линейное интерполирование (h=1) возможно. Интерполяционные формулы Ньютона используют лишь значения функций, лежащие лишь по одну сторону от выбранного начального значения Для интерполирования в середине таблицы удобно применять формулы, содержащие как последующие, так и предшествующие значения функций по отношению к начальному ее значению. При этом используются центральные разности Интерполяционные формулы, построенные с помощью центральных разностей - это формулы Гаусса, Стирлинга, Бесселя.
|
- равноотстоящие причем 
то, пологая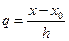 
, получим остаточные члены для 1-ой и 2-ой интерполяционных формул Ньютона:
(10)
, (11)
- некоторое промежуточное значение между узлом интерполирования 
.
, для экстраполирования возможно, что 
).
. Учитывая, что h достаточно мало и 
(12)
. Возможно ли линейное программирование с той же степенью точности?
, то 
где 
, а 
(интерполируем не далее, чем на 1 шаг), то 
