Интерполяционная формула Лагранжа
Для произвольно заданных узлов интерполирования (в том числе и для неравноотстоящих узлов) применяется интерполяционная формула Лагранжа.
Требуется построить полином
Рис. 4.2 Построение полинома что
Рассмотрим частную задачу: построить полином при Т.е. Такой полином имеет вид:
При поэтому И В результате получаем:
Будем теперь искать интерполяционный полином в виде
Этот полином имеет вид:
Подставляя (15) в (16), получаем:
Это и есть интерполяционная формула Лагранжа
При n=1 имеем:
проходящей через 2 заданные точки: ( При n=2 получаем уравнение параболы, проходящей через три точки:
(точки Пример: Для функции Решение: Вычисляем По формуле (17) получаем:
Точность не велика, т.к. синусоиду мы интерполируем квадратичной параболой.
Оценка погрешности интерполяционной формулы Лагранжа
где
Пример: с какой точностью можно вычислить Решение:имеем
Из формулы (18) получаем:
|

 Пусть на отрезке [a, b] задано n+1 значений аргумента и известны значения функций y=f(x):
Пусть на отрезке [a, b] задано n+1 значений аргумента и известны значения функций y=f(x):

 степени не выше n, имеющий в заданных узлах
степени не выше n, имеющий в заданных узлах  , те же значения, что и функция f(x), т.е. такой,
, те же значения, что и функция f(x), т.е. такой,

 , такой, чтобы
, такой, чтобы  = 0
= 0 и
и 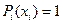 при
при 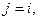
 (13)
(13) (14)
(14) в силу условия (13),
в силу условия (13),

 (15)
(15)
 (16)
(16) (17)
(17)

 - уравнение прямой,
- уравнение прямой,
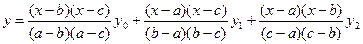
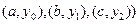
 построить интерполяционный полином Лагранжа, выбрав узлы:
построить интерполяционный полином Лагранжа, выбрав узлы: 



 (18)
(18)
 с помощью интерполяционной формулы Лагранжа для функции
с помощью интерполяционной формулы Лагранжа для функции  , выбрав узлы интерполирования
, выбрав узлы интерполирования  Три точки n=2.
Три точки n=2. Отсюда
Отсюда  (т.к.
(т.к. 




