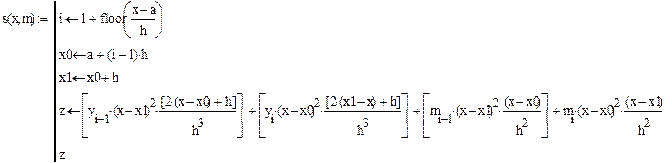Вспомогательные материалы
1. Пример выполнения работы (пункт 1) Пусть задана функция y = sin x на интервале [ 1.15, 1.19 ]
При задании с шагом 0.2 таблица примет вид:
Интерполяционный полином Лагранжа для трех узлов имеет вид
Вычислим по данной формуле значение в точке x = 1.16. Имеем: x(0) = 1.15; x(1) = 1.17; x(2) = 1.19; y(0) =0.9128; y(1) = 0.9208; y(2) = 0.9284 Подставляя данные в выражение для L(x), получаем
Полученное значение точно совпадает с табличным для x = 1.16.
Оценим погрешность интерполирования по формуле (2). Имеем n = 2. f (n + 1) = -cos (x) Максимальное значение косинуса не превосходит 1. Следовательно, М n +1 равно 1.
Следовательно, результат интерполирования совпадает с точным значением функции до пяти знаков после запятой. Разработка программы на Mathcadе трудностей не представляет.
2. Пункт 2 задания выполняется аналогично. 3. Пример Mathcad – программы для построения кубического сплайна приведен ниже.
Контрольные вопросы 1.Чему равно значение интерполяционного полинома в узловых точках? 2. Какова максимальная степень многочлена Лагранжа? 3. Какова максимальная степень многочлена Ньютона? 4. Как оценивается погрешность интерполяции? 5. В чем состоит различие сплайн – интерполирования от обычной интерполяции? Раздел 5
|







 = 0.5 * 10 - 6.
= 0.5 * 10 - 6.