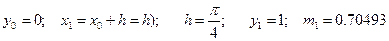Обратное интерполирование
Задача обратного интерполирования: по заданному значению функции Предположим, что на отрезке [a, b], содержащем узлы интерполяции, функция f(x) монотонна. Тогда существует однозначная обратная функция x=F(y). Она задана той же таблицей, что и y=f(x), только теперь аргументом будет значение В этом случае обратное интерполирование сводится к обычному интерполированию для функции x=F(y). Т.е. строится интерполяционный многочлен (например, по формуле Лагранжа) – многочлен Второй способ применим ко всякой функции f(x) (не обязательно к монотонной). Не меняя ролями функцию и аргумент, записываем по какой – либо формуле интерполяционный многочлен 7. Сплайн – интерполяция. (spline – рейка, планка) Механические сплайны – гибкие деревянные рейки, закрепленные на концах. В узлах (точках) интерполяции подвешивают грузила. Сплайн принимает форму, минимизирующую его потенциальную энергию. Если сплайн представить функцией S(x), то S и Кубическая сплайн – функция, удовлетворяющая условиям Т.е. кубический сплайн есть самая гладкая из функций, интерполирующих заданные точки. Пусть отрезок [a, b] разбит на n частей точками Сплайном k-ой степени называется функция, представляющая собой многочлен не выше к-ой степени на каждом из последовательно примыкающих друг к другу интервалов Сплайн 1-ой степени – кусочно-линейная функция (непрерывная). Производная терпит разрыв в точках излома. Задача интерполяции функции Значения сплайна в узлах интерполяции
В сплайне (19) неизвестные Уравнения (20) – (23) дают 4n – 2 уравнения. Т.о. для определения величин
Построим сплайн, удовлетворяющий краевым условиям I типа. Введем величины Интерполяционный кубический сплайн вида
где Из условия (23) и краевых условий (I) можно определить параметры Действительно, легко проверить, подставляя
Беря вторые производные от S(x) по х и подставляя
И краевых условий (I) и условий (25) получим систему из n+1 линейных уравнений относительно неизвестных Из равенства
В результате имеем:
Решая систему (28) методом Гаусса, получаем в результате прямого хода коэффициенты:
После обратного хода (обратной прогонки) получаем результат:
Результаты (29) и (30) позволяют построить кубический сплайн. Построение сплайна с учетом краевых условий (II) производится аналогично. Точность интерполяционной функции f(x), имеющей на отрезке [a, b] непрерывные производные до 3-его порядка включительно, кубическим сплайном S(x) по точкам равномерного разбиения отрезка с шагом h при любых краевых условиях (I – III), оценивается неравенством:
Неравенство (31) дает завышенную оценку точности. Пример: На отрезке [0,
С помощью интерполяционной формулы вычислить приближенное значение
Решение: Т.к. задано 2 отрезка, то представим сплайн в виде:
Краевые условия (I) имеют вид:
Из системы уравнений (28) имеем:
Находим
Подставляем значения
(т.к. Аналогично:
Получаем для
Т. о.
|

 найти аргумент
найти аргумент  , при котором
, при котором  . Функция y=f(x) задана таблично.
. Функция y=f(x) задана таблично. , а
, а  -соответствующее значение функции.
-соответствующее значение функции. . При подстановке в
. При подстановке в  .
. . Неизвестное значение
. Неизвестное значение  . Если число узлов велико, то этот способ нахождения
. Если число узлов велико, то этот способ нахождения  непрерывны на [
непрерывны на [  ].
].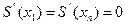 называется естественным кубическим сплайном. С математической точки зрения кубическая сплайн – функция – единственная функция, обладающая свойством минимальной кривизны, среди всех функций, интерполирующих данные точки и имеющих квадратичную интегрируемую вторую производную.
называется естественным кубическим сплайном. С математической точки зрения кубическая сплайн – функция – единственная функция, обладающая свойством минимальной кривизны, среди всех функций, интерполирующих данные точки и имеющих квадратичную интегрируемую вторую производную.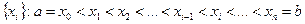

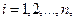 причем в точках стыка двух интервалов
причем в точках стыка двух интервалов 
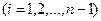 функция непрерывна вместе со своими производными до порядка не выше к
функция непрерывна вместе со своими производными до порядка не выше к на отрезке [a, b] кубическим сплайном (сплайном 3-ей степени) состоит в нахождении функции S(x), равной многочлену третьей степени
на отрезке [a, b] кубическим сплайном (сплайном 3-ей степени) состоит в нахождении функции S(x), равной многочлену третьей степени  на каждом отрезке
на каждом отрезке  т.е.
т.е. 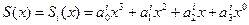
 (19)
(19) и сплайн-функция S(x) непрерывна в узлах интерполяции вместе с производными первого и второго порядков.
и сплайн-функция S(x) непрерывна в узлах интерполяции вместе с производными первого и второго порядков.




 . Интервал [a, b] разбит на n участков. Т. о. имеем 4n неизвестных: (i*p) = 4n.
. Интервал [a, b] разбит на n участков. Т. о. имеем 4n неизвестных: (i*p) = 4n.
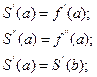

 , называемые наклонами сплайна в узлах
, называемые наклонами сплайна в узлах  (24)
(24)
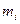
 в (24) и т.д., что
в (24) и т.д., что
 и
и  , получаем
, получаем
 (25)
(25) получаем
получаем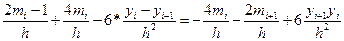
 (26)
(26)


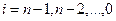 (30)
(30) где
где  (31)
(31)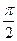 ] построить кубический сплайн с шагом
] построить кубический сплайн с шагом  , интерполирующий функцию
, интерполирующий функцию  , если заданы значения функции в трех узлах интерполяции:
, если заданы значения функции в трех узлах интерполяции:


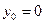



 и сравнить с точным значением 0,5.
и сравнить с точным значением 0,5.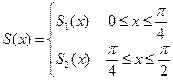
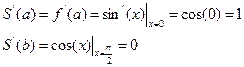




 в (24). Получаем:
в (24). Получаем:
 и числа, содержащие
и числа, содержащие 

 : (т.к.
: (т.к.