Решение систем линейных алгебраических уравнений методом итераций
Рассмотрим систему линейных алгебраических уравнений
Если все диагональные элементы
где
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы: Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы:
Рис. 2.1 Блок-схема решения системы линейных алгебраических уравнений Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Из неравенства (13) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности e. Отклонение приближения
Для вывода (14) достаточно рассмотреть равенства:
Далее И учитывая, что В неравенствах (13) и (14) используются согласованные нормы для матриц и векторов, т.е. m и l-нормы. Неравенство (14) дает завышенную оценку числа итераций k. Из (14) можно получить удобное условие, позволяющее принять приближение
Пример:Найти решение системы уравнений
методом итераций с точностью 10-2. Решение:Приведем систему к виду (10)
Запишем последовательность итераций
Для приведенной матрицы
В качестве начального приближения возьмем вектор-столбец свободных членов приведенной системы Число итераций для достижения заданной точности
Вычислим теперь три последовательных приближения по формулам (15) и оценим погрешность каждого результата, используя неравенство (13) в виде:
Первое приближение:
Следовательно,
Далее последовательно находим:
Третья итерация:
Заданная точность достигается за 5 шагов. Точное решение Ниже приведена блок – схема алгоритма решения системы линейных алгебраических уравнений методом итераций.
Лабораторная работа 2
|

 (9)
(9)
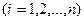 , то систему (1) можно представить в приведенном виде
, то систему (1) можно представить в приведенном виде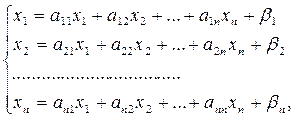 (10)
(10)




 (11)
(11) возьмем вектор b и подставим его в уравнение (11). Получим
возьмем вектор b и подставим его в уравнение (11). Получим  .Продолжая процесс, получим последовательности приближений:
.Продолжая процесс, получим последовательности приближений: - первое приближение
- первое приближение -второе приближение (12)
-второе приближение (12) - (k+1)-ое приближение.
- (k+1)-ое приближение. то, переходя к пределу в равенстве
то, переходя к пределу в равенстве  , убеждаемся, что x является решением уравнения (11), т.е.
, убеждаемся, что x является решением уравнения (11), т.е.
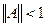 , то уравнение (11) имеет единственное решение x, к которому стремится последовательность итераций (12) при любом выборе начального приближения.
, то уравнение (11) имеет единственное решение x, к которому стремится последовательность итераций (12) при любом выборе начального приближения.
 понимают следующие выражения:
понимают следующие выражения: (m-норма) сумма модулей элементов строки
(m-норма) сумма модулей элементов строки (l-норма) сумма модулей элементов столбца
(l-норма) сумма модулей элементов столбца (k-норма)
(k-норма)



 . Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством
. Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством , (13)
, (13) - норма вектора X
- норма вектора X m-норма или кубическая норма
m-норма или кубическая норма l-норма или октаэдрическая норма
l-норма или октаэдрическая норма -второе приближение (12)
-второе приближение (12)

 понимают следующие выражения:
понимают следующие выражения: (m-норма) сумма модулей элементов строки
(m-норма) сумма модулей элементов строки (l-норма) сумма модулей элементов столбца
(l-норма) сумма модулей элементов столбца (k-норма)
(k-норма)

 . Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством
. Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством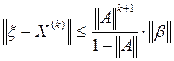 , (13)
, (13) - норма вектора X
- норма вектора X l-норма или октаэдрическая норма
l-норма или октаэдрическая норма k-норма или сферическая норма.
k-норма или сферическая норма. от решения x по норме не будет превышать e, если
от решения x по норме не будет превышать e, если (14)
(14) ;
;  ;
; 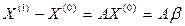 ;
; ;
; ; и т.д.
; и т.д.
 .
. , т.к. норма
, т.к. норма 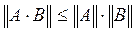 .
. (15)
(15)

 (16)
(16)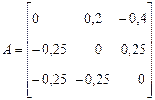 достаточное условие ходимости выполняется по m-норме:
достаточное условие ходимости выполняется по m-норме: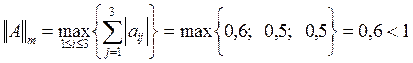
 .
. определяем из неравенства (13)
определяем из неравенства (13)  , которое запишем так:
, которое запишем так: , действительно:
, действительно: 
 .
. ;
;  т.к.
т.к.  то
то  ;
;  .
.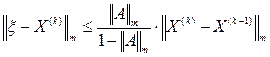 .
. 


 дает значение корня ξ с погрешностью, не превышающей величины
дает значение корня ξ с погрешностью, не превышающей величины  .
.
 ;
; 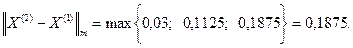
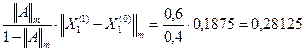

 ;
; 

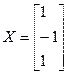 .
.









