Погрешности вычислений
Краткое введение. Большинство величин, с которыми приходится встречаться в практике, являются приближенными, т.е. такими, точное значение которых неизвестно. Оценкой приближения такой величины к точному значению является погрешность, или ошибка. В практике используют абсолютные и относительные погрешности. Абсолютная погрешность ε;- это разность между истинным и приближенным значением величины:
Относительная погрешность - это отношение величины абсолютной погрешности к приближению:
Для величин, близких по значению к единице, абсолютная и относительная погрешности имеют один порядок. Для очень больших и очень маленьких величин эти погрешности существенно отличаются. Например, если точное значение некоторой величины равно 0.00006, а приближенное значение 0.00005, то Если с приближенными значениями проводить различные арифметические действия, то в результате получится приближенная величина, погрешность которой будет зависеть от погрешностей исходных величин и, как правило, будет больше этих величин. Погрешности будут вычисляться следующим образом:
СЛОЖЕНИЕ (ВЫЧИТАНИЕ)
УМНОЖЕНИЕ
ДЕЛЕНИЕ
Для уменьшения погрешности в практической деятельности рекомендуется соблюдать следующие правила: 1) По необходимости избегать вычитания двух почти равных чисел. 2) Использовать формулы типа a(b-c) = ab -ac; (b-c)/a = b/a - c/a.
|

 (1)
(1)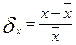 (2)
(2)
 =
=  , а
, а  ( 20%). Если точное значение величины равно 100500, а приближенное 100000, то
( 20%). Если точное значение величины равно 100500, а приближенное 100000, то  , а
, а  .
.
 (3)
(3)
 (4)
(4)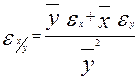
 (5)
(5)


