Собственно-корреляционные параметрические методы изучения связи.
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
где
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: Таблица 8.5
|
(8.5)
(8.6)
(8.7)
- коэффициент регрессии в уравнении связи;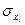
- среднеквадратическое отклонение соответствующего, статистически существенного, факторного признака.
. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице:
