Оценка линейного коэффициента корреляции
Пример: На основе выборочных данных о деловой активности однотипных коммерческих структур оценить тесноту связи между прибылью у (млн. руб.) и затратами на 1 руб. произведенной продукции x (коп.).
Таблица 8.6 Расчетная таблица для определения коэффициента корреляции
1. Используя формулу (8.5) получаем:
2. По формуле (8.6) значение коэффициента корреляции составило:
Таким образом, результат по всем формулам одинаков и свидетельствует о сильной обратной зависимости между изучаемыми признаками.
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда
где
Все эти дисперсии есть дисперсии результативного признака. Теоретическое корреляционное отношение определяется по формуле:
где
Корреляционное отношение изменяется в пределах от 0 до 1
Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:
где Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: Приближение На основе данных таблицы 8.4 рассчитаем коэффициент множественной корреляции и его ошибку:
Множественный коэффициент корреляции составит:
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками
В случае зависимости
где В первом случае исключено влияние факторного признака На основании приведенных выше данных о зависимости трех факторов деятельности предприятий вычислим частные коэффициенты корреляции (см. табл. 8.4):
|





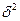 характеризует отклонения групповых средних результативного показателя от общей средней:
характеризует отклонения групповых средних результативного показателя от общей средней: (8.8)
(8.8) - корреляционное отношение;
- корреляционное отношение;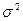 - общая дисперсия;
- общая дисперсия; - средняя из частных (групповых) дисперсий;
- средняя из частных (групповых) дисперсий; - межгрупповая дисперсия (дисперсия групповых средних).
- межгрупповая дисперсия (дисперсия групповых средних). (8.9)
(8.9) - дисперсия эмпирических (фактических) значений результативного признака.
- дисперсия эмпирических (фактических) значений результативного признака. и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 8.1).
и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 8.1). (8.10)
(8.10) - парные коэффициенты корреляции между признаками.
- парные коэффициенты корреляции между признаками. .
.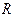 к единице свидетельствует о сильной зависимости между признаками.
к единице свидетельствует о сильной зависимости между признаками. ;
;  ;
; 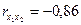 .
.
 и
и  при фиксированном значении других
при фиксированном значении других  факторных признаков, то есть когда влияние
факторных признаков, то есть когда влияние  исключается, то есть оценивается связь между
исключается, то есть оценивается связь между  от двух факторных признаков
от двух факторных признаков 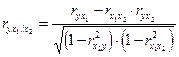
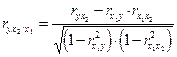 (8.11)
(8.11) - парные коэффициенты корреляции между указанными в индексе переменными.
- парные коэффициенты корреляции между указанными в индексе переменными.
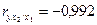 ;
;  .
.


