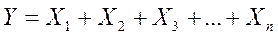Жестко детерминированные модели факторного анализа.

Эти модели приобрели достаточно широкое распространение, особенно в рамках традиционного ретроспективного анализа. Анализ с помощью жестко детерминированных факторных моделей, иногда называемый сокращенно детерминированным анализом, имеет ряд особенностей.

Во-первых, при детерминированном подходе факторная модель полностью замыкается на ту систему факторов, которые поддаются объединению в данную модель. Границей составления такой модели является длина непрерывной цепи прямых связей.

Во-вторых, данный подход не позволяет разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели. Таким образом, исследователь условно абстрагируется от действия других факторов, а все изменения результативного показателя полностью приписываются влиянию факторов, включенных в модель.

В-третьих, детерминированный анализ может выполняться для единичного объекта в отсутствии совокупности наблюдений.

Жестко детерминированная факторная модель называется полной, если результативный показатель количественный, и неполной, если результативный признак качественный. Для примера можно привести такие модели:

- полная модель:

- неполная модель:

В полной двухфакторной модели один фактор всегда количественный, второй — качественный. В этом случае, как это принято в отечественной статистике, замену факторов рекомендуют начинать с количественного показателя. (Напомним, что в нашей стране до настоящего времени до­минирует правило, согласно которому при расчете агрегатных индексов принято взвешивать индексируемый показатель по весам отчетного периода этому правилу и соответствует порядок замены факторов, начиная с количественного.

Виды моделей детерминированного анализа:

- аддитивная - модель сложения:

- мультипликативная - модель умножения:

- кратная - модель деления:

 

- смешанная,

Моделирование аддитивных факторных систем осуществляется за счет расчленения одного или нескольких факторных показателей на составные элементы.

Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы сомножители.

К кратным моделям применяют следующие способы их преобразования:

удлинения; формального разложения; расширения; сокращения.

1. Удлинение факторной модели - предусматривает удлинение числителя исходной
модели путем замены одного или нескольких факторов на сумму однородных показателей.

2. Способ формального разложения - предусматривает удлинение знаменателя исходной факторной системы путем замены одного или нескольких факторов на сумму или произведение однородных показателей.

3. Метод расширения предусматривает расширение исходной факторной модели за счет «X» числителя и знаменателя на один или несколько новых показателей

4. Способ сокращения - создает новый фактор системы путем деления числителя и знаменателя на один и тот же показатель.

Достаточно широкое распространение в факторном анализе имеют многофакторные мультипликативные модели (ММ). Можно сформулировать некоторые правила построения таких моделей:

1. ММ должна быть экономически обоснована, т.е. место фактора в модели должно соответствовать его экономической роли в формировании результативного признака.

2. ММ целесообразно строить из двухфакторной полной модели путем последовательного расчленения факторов (как правило, качественных) на составляющие; при очередном расширении модели необходимо тщательно следить за соблюдением связи «причина — следствие».

3. Мм должна быть такой, чтобы факторы можно было укрупнять (свертка модели) и слева направо, и справа налево, а произведение двух любых стоящих рядом факторов давало бы экономически понятный фактор более высокого порядка.

4Лосгроение неполной ММ в большинстве случаев рекомендуется начинать с построения и последующей детализации соответствующей полной модели.

5.При написании формулы ММ факторы в модели рекомендуется располагать в порядке их замены слева направо.