Классическая теория теплоемкости твердых тел
Рассмотрим диапазон температур, далекий от нуля и температуры плавления. Колеблющийся атом (или ион) в кристаллической решетке обладает 3 степенями свободы. На каждую колебательную степень свободы в среднем приходится энергия, равная kT (сумма двух половинок kT – одна в виде кинетической и одна в виде потенциальной энергии). Следовательно, энергия колебательного движения 1 атома (иона) в кристаллической решетке равна áeñ = 3kT. Внутренняя энергия одного моля твердого тела равна U = NA áeñ = 3kNAT = 3RT. Поскольку объем твердых тел при нагревании изменяется мало, их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, и говорят просто о молярной теплоемкости твердого тела, которая равна CV» Cp = C = dU/dT = 3R» 25 Дж/(моль×К). Мы пришли к закону Дюлонга и Пти: атомная (молярная) теплоемкость всех (химически простых кристаллических) твердых тел при достаточно высокой температуре одинакова, равна 3R и не зависит от температуры. Данный закон выполняется с довольно хорошим приближением для многих химических элементов при комнатной температуре. Однако для бериллия, бора, кремния и алмаза теплоемкость значительно меньше. Это означает, что: 1) на самом деле теплоемкость зависит от температуры; 2) комнатные температуры для бериллия, бора, кремния и алмаза не являются достаточно высокими (например, у алмаза молярная теплоемкость С» 3R при температуре t» 1800 °C). Если твердое тело является химическим соединением (например, NaCl, MnS), то надо учитывать порознь ионы Na+ и Cl -, колеблющиеся независимо друг от друга, и справедлив закон Джоуля-Коппа: молярная теплоемкость твердого соединения равна сумме атомных теплоемкостей элементов, из которых оно состоит, т.е. равна 3Rn, где n – число атомов в молекуле (для двухатомных кристаллов С = 6R, для трехатомных кристаллов С = 9R¼). 28. Понятие о квантовой статистике. Распределения Бозе-Эйнштейна и Ферми-Дирака. Энергия Ферми
Квантовая статистика – раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики. При рассмотрении системы многих частиц в классической статистической физике (распределения Максвелла и Больцмана) предполагалось, что частицу можно отличить от всех таких же частиц. Например, если две частицы поменяются местами, то получится новое микросостояние. Квантовая статистика строится на принципе неразличимости тождественных частиц: все одинаковые частицы (например, все электроны в металлах, все протоны в ядрах атомов) считаются принципиально неразличимыми друг от друга. Если частицы поменяются местами друг с другом, то получится исходное микросостояние. (Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел: главного, орбитального, магнитного и магнитного спинового. Распределение электронов в атоме подчиняется принципу Паули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел.) Все элементарные частицы разделяются на два класса. К одному классу относятся электроны, протоны, нейтроны и все частицы с полуцелым спином. Эти частицы подчиняются квантовой статистике Ферми-Дирака и поэтому называются фермионами. Фермионы подчиняются принципу Паули, и в данном квантовом состоянии системы фермионов не может находиться более одной частицы. (Аналогия: в одном месте пространства не может находиться больше одного непроницаемого твердого тела.) К другому классу относятся фотоны, фононы, p- и К-мезоны и все частицы с целым спином. Системы таких частиц описываются квантовой статистикой Бозе-Эйнштейна и поэтому называются бозонами. Бозоны не подчиняются принципу Паули: в каждом квантовом состоянии может находиться любое число частиц. (Аналогия: в одном месте пространства возможно одновременное пребывание облаков пара или дыма, лучей света, звуковых волн.) Основной в квантовой статистике является задача о распределении частиц по координатам и скоростям (энергиям) и нахождении средних значений величин, характеризующих рассматриваемую систему. Для нахождения общего числа всех возможных квантовых состояний системы из N частиц вводится понятие 6N-мерного фазового пространства, так как состояние системы определяется заданием 6N переменных, поскольку состояние каждой частицы определяется тройкой координат x, y, z и тройкой соответствующих проекций импульса px, py, pz. Число частиц, которые могут находиться в одном квантовом состоянии, определяется числами заполнения Ni. Для бозонов числа заполнения могут принимать любые целые значения Ni = 0, 1, 2, 3... Для фермионов возможны только два числа: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц в системе. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии áNiñ. Для этого были получены следующие функции распределения:
В приведенных формулах: k – постоянная Больцмана; Т – термодинамическая температура. Величина m = (U – TS + pV) / N называется химическим потенциалом, отнесенным к отдельной частице (U – внутренняя энергия системы; S – ее энтропия; V – объем системы; р – давление). Для бозонов m £ 0, так как иначе получается (из функции распределения), что среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Система частиц (в частности, идеальный газ) называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Параметром вырождения называется величина Условие малости вырождения имеет вид Температурой вырождения ТВ называется температура, при которой вырождение становится существенным. Ниже этой температуры отчетливо проявляются квантовые свойства системы частиц. Если Т >> ТВ, то поведение системы частиц (газа) описывается классическими законами. Температура ТВ определяется из условия А = 1:
Вырождение газов становится существенным при очень низких температурах и больших плотностях. Например, для водорода при нормальных условиях (Т = 300 К и n0» 3 ×1025 м-3) параметр вырождения А» 3 ×10-5 << 1. Температура вырождения для водорода ТВ» 1 К. Для всех остальных газов, более тяжелых, чем водород, величина А еще меньше. Поэтому газы при нормальных условиях не бывают вырожденными и описываются классической статистикой Максвелла-Больцмана.
Для электронов (фермионов) среднее число частиц в квантовом состоянии и вероятность заполнения квантового состояния (от 0 до 1) совпадают. Графики функций Ферми-Дирака для температур Т = 0 и Т > 0 показаны на рис. 83. Такое распределение обусловливается необходимостью соблюдения двух требований: во-первых, полная энергия должна быть минимальной, и, во-вторых, должен соблюдаться принцип Паули. Поэтому при Т = 0 все электроны не могут находиться на самом минимальном энергетическом уровне. Они начинают заполнять квантовые состояния с самого нижнего энергетического уровня, последовательно занимая более высокие квантовые состояния, причем каждое из них лишь одним электроном. Последний электрон занимает уровень с максимальной энергией. Этот уровень называется уровнем Ферми, а энергия уровня – энергией Ферми ЕF. При Т = 0 функция разрывная. При E < EF функция fФ = 1, т.е. все квантовые состояния с такими энергиями заполнены электронами. При E > EF функция fФ = 0, т.е. все квантовые состояния свободны. При этом ЕF = m, и распределение Ферми-Дирака обычно записывается в виде
Однако такое наглядное определение энергии Ферми имеет смысл лишь в применении к свободным электронам в металле. В общем случае такое определение не точно. Например, в диэлектриках и во многих полупроводниках энергетический уровень Ферми располагается примерно в середине запрещенной зоны, где заведомо нет разрешенных энергетических уровней электронов. Поэтому более общее определение гласит: уровень Ферми– это такой энергетический уровень, вероятность заполнения которого электроном равна 1/2. Это следует из последней формулы при подстановке в нее энергии Е равной EF. При температурах Т > 0 функция распределения fФ плавно изменяется ("размывается") от 1 до 0 в узкой области (порядка нескольких kT) в окрестности EF. Причина такого "размытия" в том, что небольшая часть электронов получает дополнительную энергию за счет взаимодействия с тепловыми колебаниями кристаллической решетки. Поскольку средняя энергия теплового движения атомов имеет порядок kT, то и область изменения энергии электронов вблизи уровня Ферми также имеет порядок нескольких kT. В самом деле, подсчитаем значение fФ(Е) для энергий Е отличающихся от EF на ±3kT (т.е. E – EF = ±3kT):
В тепловом движении участвует лишь небольшое число электронов, например, при комнатной температуре Т» 300 К – это 10 - 5 от общего числа электронов.
29. Понятие о квантовой теории теплоемкости. Теории Эйнштейна и Дебая. Фононы
Классическая теория теплоемкости имеет ограниченное применение, так как ее теоретические выводы не всегда согласуются с экспериментом. Классическая теория не дает объяснения зависимости теплоемкости газов от температуры. Из простых формул для расчета теплоемкостей (Cp = (i + 2) R/2 и CV = iR/2) следует, что молярные теплоемкости газов определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение справедливо только для одноатомных и многих двухатомных газов (Н2, О2, N2) при комнатной температуре. У трехатомных газов наблюдается сильное отклонение теории и эксперимента. Рассмотрим температурную зависимость теплоемкости CV для водорода, которая показана на рис. 84. Из графика видно, что при повышении температуры происходит как бы "включение" различных степеней свободы: при малой температуре включаются лишь поступательные степени свободы, а затем вращательные и колебательные. Это явление объясняет квантовая механика, согласно которой энергия может принимать не любое значение, а только дискретный ряд значений. Энергия может меняться только скачками. Упрощенная схема уровней энергии (вращательных и колебательных) схематически представлена на рис. 85. При низких температурах энергия теплового движения меньше разности энергий соседних уровней (kT << De), и при столкновениях молекул вращательные и колебательные степени свободы не возбуждаются. Поведение двухатомного газа подобно одноатомному. Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными (DeВРАЩ << DeКОЛЕБ), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости.
Классическая теория теплоемкости не объясняеттемпературную зависимость молярной теплоемкости С твердых тел, показанную на рис. 86, которая в области низких температур пропорциональна кубу температуры.
Внутренняя энергия 1 моля твердого тела (с учетом 3 степеней свободы колебаний атома в узле решетки) выражается следующим образом:
Для нахождения молярной теплоемкости необходимо взять производную
Если ввести характеристическую температуру Эйнштейна
Полученная формула Эйнштейна лишь качественно описывает зависимость теплоемкости твердых тел от температуры: при высоких температурах (hn << kT) теплоемкость С ® 3R, а при Т ® 0 теплоемкость С ® 0. Однако количественно поведение теплоемкости твердого тела вблизи абсолютного нуля описывается недостаточно точно. Дебай развил упрощенную теорию Эйнштейна. В теории Дебая учтено, что колебания атомов в кристаллической решетке не являются независимыми. Между атомами твердого тела имеются настолько сильные взаимодействия, что все N частиц тела образуют связанную систему, обладающую 3N степенями свободы, причем колебания всех атомов могут происходить с разными частотами. Рассматривая непрерывный спектр частот осцилляторов, Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам звукового (или ультразвукового) диапазона. Связь между частицами в кристаллической решетке приводит к тому, что в кристалле распространяются упругие волны. Упругие волны в кристалле имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция – квант энергии волны с данной частотой n. Это позволяет сопоставить волне с частотой n квазичастицы фононы, распространению которых со скоростью звука υ соответствует звуковая волна. Фононы обладают энергией E = hn. Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке – он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе. Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе-Эйнштейна, так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным. Поэтому химический потенциал фононного газа равен нулю. При вычислении внутренней энергии кристалла и его теплоемкости вводится характеристическая температура Дебая:
– верхняя граница частот фононов, вносящих вклад в энергию тепловых колебаний кристалла (максимальная частота колебаний кристаллической решетки). При расчетах рассматривают два предельных случая: а) при высоких температурах (T >> TD) в результате вычислений получается закон Дюлонга и Пти С = 3R; б) при низких температурах (T << TD) получается закон Дебая, из которого следует, что молярная теплоемкость пропорциональна кубу температуры:
заключение
Заканчивается последняя лекция по программе курса молекулярной физики. Авторы надеются, что вам стали более понятны многочисленные явления в газах, жидкостях и твердых телах. Перед вами открылся новый уровень физической науки, но одновременно, вероятно, возникли и новые вопросы о строении окружающего материального мира. Помните, что, если вам всё понятно, "…это значит только то, что вам не всё говорят…" Желаем дальнейших успехов в изучении фундаментальных наук. Рекомендуемая литература* 1. Ремизов А.Н. Курс физики: Учеб. для вузов. М.: Дрофа, 2002. 2. Грабовский Р.И. Курс физики. СПб.: Изд-во "Лань", 2002. 3. Савельев И.В. Курс общей физики: Учеб. пособие для втузов: В 5 кн. Кн. 3. Молекулярная физика и термодинамика. М.: Наука, 1998. 4. Трофимова Т.И. Курс физики. М.: Высшая школа, 2000. 5. Сивухин Д.В.Общий курс физики.Т.2. Термодинамика и молекулярная физика. М.: Физматлит; Изд-во МФТИ, 2003. 6. Кикоин А.К., Кикоин И.К.Молекулярная физика. М.: Наука, 1976. 7. Матвеев А.Н.Молекулярная физика. М.: Высшая школа, 1981. 8. Ремизов А.Н. Медицинская и биологическая физика: Учебник. 3-е изд., испр. М.: Высшая школа, 1999. 9. Гершензон Е.М. и др. Молекулярная физика: Учебник / Е.М. Гершензон, Н.Н. Малов, А.Н. Мансуров. М.: ИЦ "Академия", 2000. 10. Курс физики: Учебник для вузов / А.А. Детлаф, Б.М. Яворский. 2-е изд. М.: Высшая школа, 2000. 11. Зисман Г.А., Тодес О.М. Курс общей физики. М.: Наука, 1974. 12. Иродов И.Е.Задачи по общей физике: Учеб. пособие. СПб: Изд-во "Лань", 2001. 13. Волькенштейн В.С. Сборник задач по общему курсу физики. СПб.: Изд-во "Специальная литература"; Изд-во "Лань", 1999. 14. Савельев И.В. Сборник вопросов и задач по общей физике: Учеб. пособие для втузов. М.: ООО "Изд-во Астрель", ООО Изд-во АСТ, 2001. 15. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов. М.: Высшая школа, 1999. 16. Кассандрова О.Н., Матвеев А.Н., Попов В.П. Методика решения задач помолекулярной физике, 1982. 17. Телеснин Р.В.Молекулярная физика. М.: Высшая школа, 1973.
* Сборник задач укажет преподаватель, ведущий семинарские занятия. Учебная литература часто переиздается, поэтому допускается пользоваться литературой, выпущенной в другие годы или другими издательствами.
|


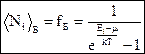

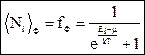
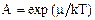 . При А << 1, т.е. при малой степени вырождения, в квантовых функциях распределений fБ и fФ можно пренебречь единицей в знаменателях и распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана:
. При А << 1, т.е. при малой степени вырождения, в квантовых функциях распределений fБ и fФ можно пренебречь единицей в знаменателях и распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана: 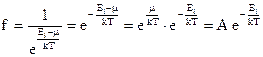 .
.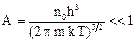 , где n0 – концентрация частиц; m – масса частиц; k – постоянная Больцмана; h – постоянная Планка; Т – термодинамическая температура.
, где n0 – концентрация частиц; m – масса частиц; k – постоянная Больцмана; h – постоянная Планка; Т – термодинамическая температура.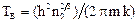 .
. Электроны проводимости в металлах являются примером вырожденного газа. В обычных условиях n0» (1028 -1029) м - 3. Так как масса электрона мала (m» 10-30 кг), то ТВ» 2000 К, т.е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден. Поэтому среднее число электронов N(E), находящихся в квантовом состоянии с энергией Е, описывается функцией распределения Ферми-Дирака:
Электроны проводимости в металлах являются примером вырожденного газа. В обычных условиях n0» (1028 -1029) м - 3. Так как масса электрона мала (m» 10-30 кг), то ТВ» 2000 К, т.е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден. Поэтому среднее число электронов N(E), находящихся в квантовом состоянии с энергией Е, описывается функцией распределения Ферми-Дирака: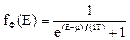 .
.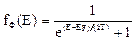 .
.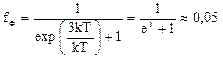 ;
;  .
. Плавные переходы на температурном графике CV между дискретными уровнями (рис. 84) объясняются тем, что согласно распределению молекул по скоростям и энергиям лишь какая-то доля молекул от общего числа первоначально имеет энергию, достаточную для возбуждения вращательного и колебательного движений.
Плавные переходы на температурном графике CV между дискретными уровнями (рис. 84) объясняются тем, что согласно распределению молекул по скоростям и энергиям лишь какая-то доля молекул от общего числа первоначально имеет энергию, достаточную для возбуждения вращательного и колебательного движений. Согласно классической теории теплоемкости теплоемкость металлов должна складываться из теплоемкости кристаллической решетки, равной 3R (закон Дюлонга и Пти), и теплоемкости электронного газа, равной 3R/2 (электрон как материальная точка имеет среднюю кинетическую энергию, равную 3kT/2). Таким образом, атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт показывает, что она равна 3R. Это объясняет квантовая механика. Известно, что функции распределения Ферми-Дирака для Т = 0 и для Т > 0 различаются лишь в узкой области энергий порядка нескольких kT. Следовательно, в процессе нагревания металла участвует лишь незначительная доля от всех электронов проводимости. Поэтому отсутствует заметная разница между теплоемкостями металлов и диэлектриков (»3R), что не могло быть объяснено классической теорией.
Согласно классической теории теплоемкости теплоемкость металлов должна складываться из теплоемкости кристаллической решетки, равной 3R (закон Дюлонга и Пти), и теплоемкости электронного газа, равной 3R/2 (электрон как материальная точка имеет среднюю кинетическую энергию, равную 3kT/2). Таким образом, атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт показывает, что она равна 3R. Это объясняет квантовая механика. Известно, что функции распределения Ферми-Дирака для Т = 0 и для Т > 0 различаются лишь в узкой области энергий порядка нескольких kT. Следовательно, в процессе нагревания металла участвует лишь незначительная доля от всех электронов проводимости. Поэтому отсутствует заметная разница между теплоемкостями металлов и диэлектриков (»3R), что не могло быть объяснено классической теорией. Простейшая квантовая теория была предложена Эйнштейном. В этой теории кристалл рассматривался как система N атомов, каждый из которых являлся квантовым гармоническим осциллятором. Колебания всех атомов происходят независимо друг от друга с одинаковой частотой n. Средняя энергия
Простейшая квантовая теория была предложена Эйнштейном. В этой теории кристалл рассматривался как система N атомов, каждый из которых являлся квантовым гармоническим осциллятором. Колебания всех атомов происходят независимо друг от друга с одинаковой частотой n. Средняя энергия 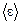 , приходящаяся на одну степень свободы атома квантового гармонического осциллятора, равна
, приходящаяся на одну степень свободы атома квантового гармонического осциллятора, равна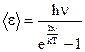 .
. .
.
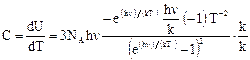
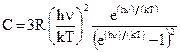 .
.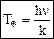 , то
, то 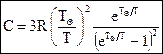 .
.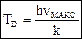 , где
, где 
 .
.



