 Явлением внутреннего трения (вязкостью) называется возникновение сил трения между слоями жидкости или газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Например, при ламинарном течении (без завихрений) скорость течения жидкости или газа в трубе изменяется по параболическому закону: скорость максимальна в центре трубы и равна нулю у стенок (рис. 18 а). Если пренебречь трением воды о воздух, то распределение скоростей слоев воды в реке будет выглядеть так, как показано на рис. 18 б.
Явлением внутреннего трения (вязкостью) называется возникновение сил трения между слоями жидкости или газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Например, при ламинарном течении (без завихрений) скорость течения жидкости или газа в трубе изменяется по параболическому закону: скорость максимальна в центре трубы и равна нулю у стенок (рис. 18 а). Если пренебречь трением воды о воздух, то распределение скоростей слоев воды в реке будет выглядеть так, как показано на рис. 18 б.
 Рассмотрим границу раздела двух соседних слоев газа (или жидкости), движущихся с разными скоростями (рис. 19). Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой F 1, направленной по течению. Более медленный слой одновременно стремится замедлить движение более быстрого слоя, действуя на него с силой F 2.
Рассмотрим границу раздела двух соседних слоев газа (или жидкости), движущихся с разными скоростями (рис. 19). Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой F 1, направленной по течению. Более медленный слой одновременно стремится замедлить движение более быстрого слоя, действуя на него с силой F 2.
 Причиной вязкости является наложение двух движений: упорядоченного движения слоев газа (или жидкости) с различными скоростями и теплового движения молекул. При этом молекулы в своем тепловом движении, переходя из слоя в слой, имеют разные скорости упорядоченного движения, и происходит перенос импульса упорядоченного движения молекул (рис. 20). Ось z на рис. 20 указывает направление потока импульса.
Причиной вязкости является наложение двух движений: упорядоченного движения слоев газа (или жидкости) с различными скоростями и теплового движения молекул. При этом молекулы в своем тепловом движении, переходя из слоя в слой, имеют разные скорости упорядоченного движения, и происходит перенос импульса упорядоченного движения молекул (рис. 20). Ось z на рис. 20 указывает направление потока импульса.
Модуль силы внутреннего трения dF, действующей на площадку dS, лежащую на границе между слоями, определяется формулой Ньютона:
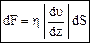 , (34)
, (34)
где h – коэффициент внутреннего трения (динамическая вязкость), dυ/dz = grad υ – градиент скорости (изменение скорости движения слоев на единицу длины в направлении нормали к поверхности слоя). Единицей динамической вязкости является паскаль-секунда (Па×с). Динамическая вязкость газов при нормальных условиях имеет порядок 10 - 5 Па×с.
Наряду с динамической вязкостью используется также кинематическая вязкость n, определяемая как отношение динамической вязкости к плотности среды: n = h/r.
Учитывая второй закон Ньютона (dP/dt = F), формулу (34) можно представить в другом виде, как поток импульса dР через площадку dS:
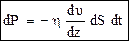 . (35)
. (35)
Знак "минус" в формуле (35) обусловлен тем, что импульс передается в направлении убывания скорости (градиент скорости отрицателен).
Из молекулярно-кинетической теории можно найти, что коэффициент вязкости для газов определяется выражением (r – плотность вещества)
 . (36)
. (36)
Расчет вязкости для жидкости чрезвычайно сложен, так как движение молекул в жидкости происходит за счет "перескоков" молекул из одного "оседлого" положения в другое. Динамическая вязкость достаточно хорошо описывается формулой вида 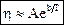 , где А и b – эмпирические постоянные, определяемые свойствами жидкости, Т – температура. Динамическая вязкость жидкостей резко уменьшается с повышением температуры (а у газов увеличивается). Динамическая вязкость обычных, не очень вязких жидкостей (вода, бензин) имеет порядок 10 - 3 Па×с.
, где А и b – эмпирические постоянные, определяемые свойствами жидкости, Т – температура. Динамическая вязкость жидкостей резко уменьшается с повышением температуры (а у газов увеличивается). Динамическая вязкость обычных, не очень вязких жидкостей (вода, бензин) имеет порядок 10 - 3 Па×с.

 Явлением внутреннего трения (вязкостью) называется возникновение сил трения между слоями жидкости или газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Например, при ламинарном течении (без завихрений) скорость течения жидкости или газа в трубе изменяется по параболическому закону: скорость максимальна в центре трубы и равна нулю у стенок (рис. 18 а). Если пренебречь трением воды о воздух, то распределение скоростей слоев воды в реке будет выглядеть так, как показано на рис. 18 б.
Явлением внутреннего трения (вязкостью) называется возникновение сил трения между слоями жидкости или газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Например, при ламинарном течении (без завихрений) скорость течения жидкости или газа в трубе изменяется по параболическому закону: скорость максимальна в центре трубы и равна нулю у стенок (рис. 18 а). Если пренебречь трением воды о воздух, то распределение скоростей слоев воды в реке будет выглядеть так, как показано на рис. 18 б. Рассмотрим границу раздела двух соседних слоев газа (или жидкости), движущихся с разными скоростями (рис. 19). Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой F 1, направленной по течению. Более медленный слой одновременно стремится замедлить движение более быстрого слоя, действуя на него с силой F 2.
Рассмотрим границу раздела двух соседних слоев газа (или жидкости), движущихся с разными скоростями (рис. 19). Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой F 1, направленной по течению. Более медленный слой одновременно стремится замедлить движение более быстрого слоя, действуя на него с силой F 2. Причиной вязкости является наложение двух движений: упорядоченного движения слоев газа (или жидкости) с различными скоростями и теплового движения молекул. При этом молекулы в своем тепловом движении, переходя из слоя в слой, имеют разные скорости упорядоченного движения, и происходит перенос импульса упорядоченного движения молекул (рис. 20). Ось z на рис. 20 указывает направление потока импульса.
Причиной вязкости является наложение двух движений: упорядоченного движения слоев газа (или жидкости) с различными скоростями и теплового движения молекул. При этом молекулы в своем тепловом движении, переходя из слоя в слой, имеют разные скорости упорядоченного движения, и происходит перенос импульса упорядоченного движения молекул (рис. 20). Ось z на рис. 20 указывает направление потока импульса.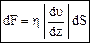 , (34)
, (34)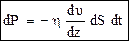 . (35)
. (35) . (36)
. (36)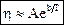 , где А и b – эмпирические постоянные, определяемые свойствами жидкости, Т – температура. Динамическая вязкость жидкостей резко уменьшается с повышением температуры (а у газов увеличивается). Динамическая вязкость обычных, не очень вязких жидкостей (вода, бензин) имеет порядок 10 - 3 Па×с.
, где А и b – эмпирические постоянные, определяемые свойствами жидкости, Т – температура. Динамическая вязкость жидкостей резко уменьшается с повышением температуры (а у газов увеличивается). Динамическая вязкость обычных, не очень вязких жидкостей (вода, бензин) имеет порядок 10 - 3 Па×с.


