Следствия.
1. Учитывая, что n = N/V, уравнение (12) можно записать в виде
Следовательно, произведение объема газа на его давление численно равно 2/3 кинетической энергии хаотического поступательного движения всех молекул газа, заключенных в этом объеме. 2. Сравним уравнение (13) с уравнением Клапейрона-Менделеева
3. Подставим в уравнение (12) известную формулу (5) p = nkT:
Отсюда следуют два вывода: а) температура – мера средней кинетической энергии движения молекул; б) постоянная Больцмана – коэффициент пропорциональности между температурой и энергией [Дж/К]. 4. Из формулы (14) можно найти среднюю квадратичную скорость:
Числом степеней свободы механической системы называется количество независимых величин (координат), с помощью которых можно определить положение системы (в пространстве). Положение материальной точки (одноатомный газ) полностью определяется тремя координатами (x, y, z) – 3 степени свободы (рис. 5). Положение абсолютно твердого тела (трехатомный и многоатомный газ) может быть задано тремя координатами центра масс (x, y, z) и тремя углами вращательного движения (a, b, j) вокруг трех пространственных осей, проходящих через центр масс (рис. 6) – 6 степеней свободы.
Двухатомная молекула (N2, H2, O2) с жесткой связью между атомами имеет 5 степеней свободы (рис. 7): 3 поступательные (x, y, z) и 2 вращательные (a, b) вокруг двух осей. Вращение вокруг третьей оси, проходящей через центры двух атомов, не меняет положение молекулы в пространстве. Формула (12) для давления газа выводилась при условии, что молекулы являются материальными точками, имеющими 3 поступательные степени свободы. Поскольку ни одна из степеней свободы не имеет преимуществ, то энергия, приходящаяся на 1 степень свободы, равна одной третьей части от áeПОСТñ. Отсюда следует закон равнораспределения: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная kT/2. При температурах в тысячи градусов связь атомов в молекуле перестает быть жесткой, атомы начинают колебаться (рис. 8). Добавляются колебательные степени свободы, которые имеют двойную энергетическую емкость (энергетический вклад), так как учитываются и кинетическая, и потенциальная энергии атомов. Итак, средняя энергия одной молекулы равна где i – число степеней свободы молекулы, равное сумме поступательных, вращательных и колебательных степеней свободы:
Формулу для внутренней энергии идеального газа можно теперь записать в общем виде: 5. Распределение Максвелла
Пусть имеется N молекул, находящихся в тепловом движении. Их скорости хаотически меняют величину и направление. Максвелл в 1860 г. показал, что, несмотря на хаотичность, существует строго определенное и однозначное распределение скоростей между молекулами.
Физический смысл F(υ): при Dυ = 1 функция Условие нормировки:
где υ – скорость на длине свободного пробега; m – масса одной молекулы; k – постоянная Больцмана; Т – температура. График функции F(υ) показан на рис. 10. Как и следовало ожидать F(υ) = 0 при υ = 0 и υ = ¥, т.е. в газе нет неподвижных молекул и движущихся с бесконечно большими скоростями. Найдем наиболее вероятную скорость υВЕР, определяющую максимум кривой распределения. Для этого следует взять производную и приравнять ее к нулю (постоянные множители при этом вынесутся за знак производной):
Корнями последнего уравнения будут:
Первые два корня – это минимумы функции F(υ), а третий корень – это максимум (наиболее вероятная скорость):
Найдем значение функции распределения в максимуме, подставив формулу (20) в уравнение (19):
Зная функцию распределения F(υ), можно найти среднюю (арифметическую) скорость:
Так, например, для температуры 300 К средние скорости молекул кислорода и водорода равны соответственно 445 м/с и 1782 м/с. Функции F(υ) можно придать другой вид, удобный при расчетах, если ввести относительную скорость: Тогда Если подставить получившиеся выражения для υ и dυ в формулу
Распределение Максвелла позволяет объяснить существование и рассеяние атмосферы планет. Чтобы покинуть Землю, молекула должна иметь скорость, превышающую вторую космическую (11,2 км/с). Эта скорость в 25 раз превышает наиболее вероятную скорость для молекул кислорода. Поэтому число покинувших Землю молекул кислорода очень мало. Однако легкие газы (водород, гелий) в основном рассеялись и остались "тяжелые" газы с небольшой скоростью молекул (азот, кислород, аргон, углекислый газ). Атмосферы сохранились у тех планет, у которых сильное тяготение (высокая вторая космическая скорость) и низкая температура (низкая скорость самих молекул). Атмосферы состоят в основном из "тяжелых" газов – азот, кислород, аммиак, метан и т.п. 6. Средняя длина свободного пробега и число столкновениЙ
Минимальное расстояние, на которое сближаются центры двух молекул при столкновении, называется эффективным диаметром молекулы d, а величина s = pd2 - эффективным сечением молекулы (рис. 13). Средняя длина свободного пробега молекулы – это прямолинейный участок пути, проходимый молекулой между двумя последовательными соударениями.
В действительности движется не одна, а все молекулы, поэтому в последнюю формулу должна входить не средняя скорость относительно стенок сосуда, а скорость относительно других молекул. Можно доказать, что áυОТНñ
Средняя длина свободного пробега l равна отношению длины пути, пройденного молекулой, к числу испытанных ею на этом пути столкновений: Таким образом, длина свободного пробега молекул тем меньше, чем больше их концентрация и эффективное сечение. Оценим порядок величин длины свободного пробега и числа соударений (т.е. необходимо найти d и n). Для нахождения d вспомним, что в жидкостях молекулы располагаются достаточно плотно друг к другу. Один моль воды (18 г) занимает объем 18 см3 = 18 × 10 - 6 м3. Разделив объем одного моля на число молекул в одном моле NA, получим приблизительно объем одной молекулы и ее линейный размер: VМОЛ При испарении воды размер молекулы d не изменяется, но теперь один моль любого газа (и водяного пара) при нормальных условиях занимает объем 22,4 ×10-3 м3. Разделив число молекул в одном моле NA на объем одного моля газа, получим концентрацию n: n = 6 ×1023 / 22,4 ×10 –3» 3 × 1025 м - 3. Подставим найденные d и n в формулу (25): l = 1 / ( Пусть средняя скорость молекулы воды (пара) равна 600 м/с. Тогда из формулы (25) можно найти число столкновений:
Естественно возникает вопрос, можно ли считать идеальным газ, в котором молекулы каждую секунду сталкиваются миллиарды раз, т.е. "взаимодействуют". Однако длина свободного пробега в 100–1000 раз больше размеров молекулы. Другими словами, время столкновения молекул примерно в 100–1000 раз меньше времени между столкновениями. Следовательно, подавляющую часть времени молекулы движутся свободно. Состояние газа в сосуде называется вакуумом, если длина свободного пробега сравнима с линейными размерами сосуда или превышает их. Газ в этом случае называют ультраразряженным. Различные степени вакуума (низкий, средний, высокий, сверхвысокий) создаются в разных технических устройствах (лампы накаливания, радиолампы, электронно-лучевые трубки телевизоров, системы вакуумного напыления металлов и т.п.).
|

 или
или  . (13)
. (13) , получим
, получим  или
или – внутренняя энергия, определяемая для одноатомного идеального газа, как энергия только поступательного движения молекул.
– внутренняя энергия, определяемая для одноатомного идеального газа, как энергия только поступательного движения молекул. , или
, или  . (14)
. (14)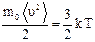 , откуда
, откуда  . (15)
. (15)
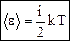 , (16)
, (16) . (17)
. (17)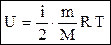 . (18)
. (18) Отложим на оси скорости все возможные скорости молекул (рис. 9). Найдем количество молекул DN, скорости которых заключены в интервале [υ, υ + Dυ]. Очевидно, это количество DN будет пропорционально общему числу молекул N, величине интервала скорости Dυ и функции распределения молекул по скоростям F(υ):
Отложим на оси скорости все возможные скорости молекул (рис. 9). Найдем количество молекул DN, скорости которых заключены в интервале [υ, υ + Dυ]. Очевидно, это количество DN будет пропорционально общему числу молекул N, величине интервала скорости Dυ и функции распределения молекул по скоростям F(υ): , или
, или  , или
, или  .
.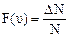 - доля частиц от общего числа, скорости которых заключены в единичном интервале вблизи скорости υ.
- доля частиц от общего числа, скорости которых заключены в единичном интервале вблизи скорости υ. , т.е. число частиц, имеющих скорости в интервале [0, ¥;], равно N (а N/N = 1).
, т.е. число частиц, имеющих скорости в интервале [0, ¥;], равно N (а N/N = 1). Одна из форм записи функции распределения Максвелла имеет вид:
Одна из форм записи функции распределения Максвелла имеет вид: , (19)
, (19) ,
, ,
, .
. ,
,  ,
,  .
. . (20)
. (20) ,
,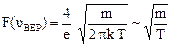 . (21)
. (21) Из формул (20) и (21) следует, что при увеличении температуры или уменьшении массы молекулы максимум кривой смещается вправо и становится ниже (рис. 11). Однако, площадь под кривой из условия нормировки (S = 1) сохраняется.
Из формул (20) и (21) следует, что при увеличении температуры или уменьшении массы молекулы максимум кривой смещается вправо и становится ниже (рис. 11). Однако, площадь под кривой из условия нормировки (S = 1) сохраняется. . (22)
. (22) .
. ,
, 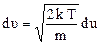 .
. , то можно получить функцию распределения F(u) для относительной скорости:
, то можно получить функцию распределения F(u) для относительной скорости: ,
, , где
, где  . (23)
. (23) У 70% всех молекул скорость отличается от наиболее вероятной не более чем на 50% (рис. 12). А скорости, превышающие наиболее вероятную более чем в 5 раз, наблюдаются у одной из 12 млрд молекул.
У 70% всех молекул скорость отличается от наиболее вероятной не более чем на 50% (рис. 12). А скорости, превышающие наиболее вероятную более чем в 5 раз, наблюдаются у одной из 12 млрд молекул.
 Пусть имеется газ с концентрацией n и движется только одна молекула, а остальные неподвижны. За 1 с эта молекула пройдет путь, равный ее средней скорости áυñ, и столкнется со всеми молекулами, центры которых расположены в ломаном цилиндре длиной áυñ и площадью основания, равной эффективному сечению (рис. 14). Умножив объем цилиндра на концентрацию n, получим число столкновений: n' = pd2 áυñ n.
Пусть имеется газ с концентрацией n и движется только одна молекула, а остальные неподвижны. За 1 с эта молекула пройдет путь, равный ее средней скорости áυñ, и столкнется со всеми молекулами, центры которых расположены в ломаном цилиндре длиной áυñ и площадью основания, равной эффективному сечению (рис. 14). Умножив объем цилиндра на концентрацию n, получим число столкновений: n' = pd2 áυñ n. áυñ. Поэтому, среднее число столкновений за 1 с равно:
áυñ. Поэтому, среднее число столкновений за 1 с равно: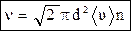 . (24)
. (24) . (25)
. (25)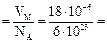 30 × 10-30 м3,
30 × 10-30 м3,  м.
м. × p × 9 ×10 –20 × 3 ×1025)» 10 - 7 м.
× p × 9 ×10 –20 × 3 ×1025)» 10 - 7 м. 6 ×10 9 c-1.
6 ×10 9 c-1.


