Ентропія. Ентропія ідеального газу
Формулу коефіцієнта корисної дії ідеальної теплової машини, що працює за циклом Карно,
приведемо до вигляду
Відношення кількості переданої Під час виконання циклу Карно зведені кількості теплоти при процесах ізотермічного розширення і стиску однакові. Розглянемо деякий оборотній цикл,
Кожну з ліній
і додамо отримані вирази:
Звідси сума зведених кількостей теплоти не залежить від шляху переходу. Це положення називається теоремою Клаузіуса. У випадку необоротної теплової машини
Тоді, об’єднавши формули для оборотної і необоротної теплових машин, маємо:
Умовимося кількість теплоти, яка віддана тілу нагрівником, вважати додатною, а кількість теплоти, віддану тілом холодильнику, – від’ємною. Тоді
причому „ = ” – відповідає оборотним переходам, а „ < ” – необоротним. В загальному вигляді
При неперервній зміні стану тіла можна вважати, що воно входить в теплообмін з неперервним рядом нагрівників і холодильників. Кожен з цих нагрівників і холодильників віддає робочому тілу або отримує від нього нескінченно малі кількості теплоти
перетворюється в інтеграл
Це співвідношення називається рівністю (нерівністю) Клаузіуса. Розглянемо оборотний цикл
Звідси,
Незалежність інтегралу
Функція стану, диференціал якої є Згідно з визначенням зміна ентропії при оборотному процесі
Ця формула визначає ентропію лише з точністю до адитивної сталої, тобто початок відліку ентропії довільний. Кожний стан тіла характеризується певним значенням ентропії S, яка є повним диференціалом. Ентропія – адитивна функція стану системи: ентропія системи дорівнює сумі ентропій всіх тіл, що входять в систему. Розглянемо фізичний зміст ентропії. Аналізуючи роботу машини, яка працює за циклом Карно, доходимо висновку, що ККД залежить від температури нагрівника. Наприклад, при однаковій температурі холодильників
тобто Це означає, що при високій температурі передачі кількості теплоти робочому тілу ефективність теплової машини зростає, тобто більша кількість переданої теплоти перетворюється в роботу. З іншого боку, зміна ентропії залежить від температури. При вищій температурі нагрівника зростання ентропії буде меншим, ніж при низькій, оскільки температура входить у знаменник виразу для ентропії. Отже, більшому зростанню ентропії відповідає зменшення ККД. Це означає, що цінність переданої нагрівником певної кількості теплоти Отже, ентропію можна розглядати як міру знецінення енергії тіла. Ентропія – міра теплової непрацездатності тіла. Розглянемо цикл
тобто інтеграл від
При необоротному процесі
менший від зміни ентропії в даному процесі. Тоді,
Для оборотного рівноважного циклу зміна ентропії
Якщо система виконує необоротний цикл, то ентропія системи зростає: Ентропія замкненої системи при будь-яких процесах, що в ній відбуваються, не може зменшуватися: Знайдемо зміну ентропії у процесах ідеального газу:
Зміна ентропії При адіабатному процесі
Для оборотного адіабатного процесу зміна ентропії дорівнює 0, для необоротного Оборотний адіабатний процес – ізоентропічний процес. При ізотермічному процесі
при ізохоричному процесі
Розглянемо, як змінюється ентропія при деяких термодинамічних процесах. На нагрівання тіла від температури
Тоді
В процесі теплообміну кількість теплоти
Оскільки
|


 і
і  .
. називається зведеною кількістю теплоти.
називається зведеною кількістю теплоти. . Проведемо ряд нескінченно близьких адіабат, які перетинають лінії прямого
. Проведемо ряд нескінченно близьких адіабат, які перетинають лінії прямого  і зворотного
і зворотного  переходів (рис. 86).
переходів (рис. 86).
 ,
,  , … кількості теплоти
, … кількості теплоти  ,
,  ,… і віддає ряду холодильників, що знаходяться при температурах
,… і віддає ряду холодильників, що знаходяться при температурах  ,
,  ,…, кількості теплоти
,…, кількості теплоти  ,
,  ,…. До кожного циклу застосуємо формулу про рівність зведених кількостей теплоти:
,…. До кожного циклу застосуємо формулу про рівність зведених кількостей теплоти: ,
,  ,…
,… .
. і
і  .
.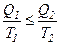 і
і  .
. ,
, .
. . Тоді сума
. Тоді сума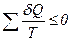
 .
.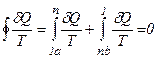 .
. .
. від виду оборотного переходу між станами 1 і 2 означає, що цей інтеграл виражає зміну деякої функції стану тіла. Підінтегральний вираз
від виду оборотного переходу між станами 1 і 2 означає, що цей інтеграл виражає зміну деякої функції стану тіла. Підінтегральний вираз  є повним диференціалом деякої функції, яка визначається лише станом системи і не залежить від виду процесу, в ході якого система прийшла в цей стан. Отже,
є повним диференціалом деякої функції, яка визначається лише станом системи і не залежить від виду процесу, в ході якого система прийшла в цей стан. Отже,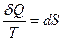 .
. .
.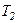 , але при різних температурах нагрівників
, але при різних температурах нагрівників 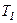 і
і 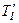 , причому
, причому 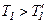 , отримаємо
, отримаємо ,
,  ,
,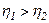 .
. ,
, ;
; 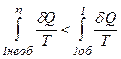 ,
, по необоротному шляху завжди менший від інтеграла по оборотному шляху між тими ж станами. Але
по необоротному шляху завжди менший від інтеграла по оборотному шляху між тими ж станами. Але ;
;  .
.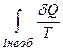
 .
. .
. .
. .
.

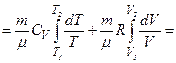
 .
. ідеального газу при переході його із стану
ідеального газу при переході його із стану  у стан
у стан 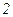 не залежить від виду процесу переходу
не залежить від виду процесу переходу  .
. і
і  – ентропія тіла зростає.
– ентропія тіла зростає. і
і  ,
, і
і  .
. .
. .
.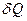 переходить від тіла з більш високою температурою
переходить від тіла з більш високою температурою  .
.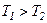 , то ентропія при теплообміні зростає.
, то ентропія при теплообміні зростає.


