Ентропія і термодинамічна ймовірність
З молекулярно-кінетичної теорії випливає, що кожному стану тіла (наприклад, газу) відповідає певний розподіл його молекул за об’ємом і певний розподіл молекул за швидкостями.
Припустимо, що в посудині перебувають лише три „мічені” молекули газу a, b, і c, які рухаються з однаковою швидкістю, а весь об’єм посудини поділено на три рівні частини І, ІІ, ІІІ (рис. 87). Різні стани газу розрізняються лише за розподілом молекул a, b, і c, по трьох комірках об’єму. Всього можливі 27 різних розподілів. Молекули газу рухаються хаотично. Якби ми спостерігали довгий час
де Ймовірність Ймовірність розподілу Отже, ймовірність будь-якого стану тіла W більша від ймовірності Термодинамічна ймовірність будь-якого стану тіла або системи дорівнює числу найрізноманітніших мікророзподілів частинок за координатами і швидкостями, які відповідають даному термодинамічному стану Найбільшу термодинамічну ймовірність має рівномірний розподіл, вона може здійснюватися найбільшою кількістю способів. Больцман встановив зв’язок між ентропією S системи і термодинамічною ймовірністю P її стану
де Отже, ентропія визначається логарифмом числа мікророзподілів частинок, за допомогою якого може бути реалізований даний макростан. Ентропія може розглядатися як міра ймовірності стану термодинамічної системи. Формула Больцмана дає змогу дати ентропії таке статистичне тлумачення: ентропія є мірою невпорядкованості системи. Ентропія досягає найбільшого значення при найбільш ймовірному стані системи. Найбільш ймовірним є стан термодинамічної рівноваги, в такому стані механічна система має мінімальну потенціальну енергію. Отже, максимум ентропії відповідає стану рівноваги ізольованої системи. Згідно із уявленнями термодинаміки процеси в замкненій системі йдуть в бік зростання ентропії до максимуму. Якщо ентропію трактувати статистично, то це означає, що процеси в замкненій системі йдуть в напрямку збільшення кількості
|


 за можливими розподілами молекул a, b, і c, то виявили би, що в середньому всі 27 розподілів зустрічаються однаково часто. Вони рівноймовірні. Під ймовірністю
за можливими розподілами молекул a, b, і c, то виявили би, що в середньому всі 27 розподілів зустрічаються однаково часто. Вони рівноймовірні. Під ймовірністю 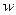 даного розподілу розуміють границю
даного розподілу розуміють границю ,
, – частина всього часу
– частина всього часу 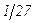 .
. , а 22-27 –
, а 22-27 – 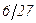 .
. , де P – термодинамічна ймовірність стану.
, де P – термодинамічна ймовірність стану.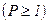 .
.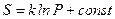 ,
, – стала Больцмана. Це співвідношення називається формулою Больцмана.
– стала Больцмана. Це співвідношення називається формулою Больцмана.


