Барометрична формула. Розподіл Больцмана
Якщо на молекули не діють зовнішні сили, то вони рівномірно розподіляються по всьому об'єму посудини і для них виконується закон розподілу Максвелла. Розглянемо тепер молекули газу, що знаходиться у полі тяжіння Землі. Якби не було тяжіння, то атмосферне повітря розсіялося б у Всесвіті внаслідок теплового руху молекул. Якби не було теплового руху, то молекули впали б на Землю. Тобто тяжіння і тепловий рух приводять до деякого стаціонарного стану газу, при якому його тиск і концентрація зменшуються з висотою. Будемо розглядати ідеальний газ, який знаходиться в однорідному полі тяжіння і температура якого постійна Т=const, тобто не змінюється з висотою. Якщо тиск газу на висоті h дорівнює Р, то на висоті h+dh він дорівнює P+dP (рис. 2.11), причому при dh >0 dP <0, оскільки тиск з висотою зменшується. Згідно із законом Паскаля (див. п. 1.7.1), різниця тисків Р i P+dP дорівнює гідростатичному тиску стовпа газу висотою dh, тобто: Р – (P+dP) = rgdh, де r – густина газу на висоті h. Використавши рівняння Менделєєва–Клапейрона, PV = mRT/M, виразимо густину r=m/V=PM/RT, звідки: dР = –
Уважаючи Т=const й інтегруючи за тиском від Po до P,а за висотою від 0 до h, отримуємо:
звідси
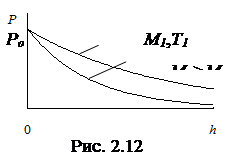
Цей вираз називається барометричною формулою, а формула для визначення висоти за зміною тиску
називається альтиметричною формулою. З цих формул можна зробити висновок, що тиск газу зменшується із висотою експоненціально (рис. 2.12) і тим швидше, чим більша молярна маса М газу і чим нижча температура Т. Барометрична формула дає можливість також визначити залежність концентрації газу від висоти. З рівняння стану ідеального газу у вигляді P=nkT при Т=const отримуємо
де no – концентрація молекул на висоті h = 0. Оскільки M = moNA, R = k moNA, то де Wn = mogh – потенціальна енергія молекули у полі тяжіння. Із збільшенням висоти концентрація молекул зменшується за експоненціальним законом. При зменшенні температури Т ®0 концентрація n ®0, тобто всі молекули опускаються на дно посудини. Больцман довів, що це співвідношення вірне не тільки для поля тяжіння, але і для інших потенціальних полів, якщо маси молекул однакові і вони знаходяться у стані теплового хаотичного руху. Тому цей вираз
|
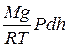, або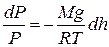
.
, 
,
.
,
,
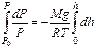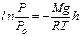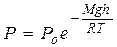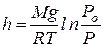
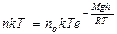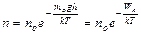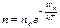називається розподілом Больцмана для частинок у зовнішньому потенціальному полі.
