Диффузия. Закон Фика. В предыдущих главах рассматривались лишь (по крайней мере, в основном) равновесные явления
В предыдущих главах рассматривались лишь (по крайней мере, в основном) равновесные явления. Напомним, это такие явления (состояния), характеристики которых не менялись в пространстве, если не было внешнего воздействия. Пример такого явления — передача теплоты. Рассмотрим теперь неравновесные явления — явления переноса. Как и для всех явлений, в которых участвует множество частиц (молекул), «генерал»-законом для явлений переноса является второе начало термодинамики. Как сказано в гл. 2, все самопроизвольно протекающие процессы идут с увеличением энтропии. Энтропия, в свою очередь (см. п. 2.4), определется числом возможных состоянийΓ. Само число возможных состояний быстро растет при выравнивании частей системы. Действительно, представим себе, что существует система из двух частей, а в каждой части — по три молекулы. Тогда число состояний в каждой части 3! = 6, а всей системы Γ0 = 6 ⋅ 6 = 36. Если же части системы потеряют свою индивидуальность и объединятся в одну систему с одинаковыми частицами, то число состояний станет Γ = 6! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 = 720. Даже если учесть, что энтропия пропорциональна lnΓ, рост впечатляет, процесс самопроизвольно протекает. Перейдем непосредственно к явлениям переноса. Если в термодинамической системе (по-простому — в газе) существует пространственная (зависящая от координат, но не от времени) неоднородность, то движение молекул самопроизвольно выравнивает эти неоднородности. Начнем с неоднородности числа частиц — концентрации n = N / V, или связанной с концентрацией плотности ρ= т 0 п. Диффузия, как явление (рис. 4.2), заключается в самопроизвольном выравнивании (концентрация n (х) зависит от координаты) концентраций. Суть явления диффузии заключается в переносе массы m (или частиц N) газа из мест с большей концентрацией n + в места с меньшей концентрацией n в результатевзаимного проникновения частиц из разных пространственных частей системы. Всякое явление переноса (в частности диффузии) характеризуется потоком
Поток считается направленным по оси х. Число частиц легко сосчитать, как это уже делалось неоднократно. (Вспомним вывод основного уравнения молекулярно-кинетической теории в гл. 1 или вывод формулы для длины свободного пробега молекулы газа в п. 4.1). Для этого выделим часть объема, из которого молекулы могут долететь за время Δ t до сечения, в котором рассматривается изменение концентрации. В этом сечении координата имеет значение х, а концентрация — значение п 0. Молекулы движутся со среднеквадратичнойскоростью
Так как молекулы движутся прямолинейно, то расстояние, которое можно взять справа и слева от выделенного сечения, не больше длины свободного пробега l, определяющейся концентрацией:
Напомню, σ — площадь сечения молекулы, табличная величина. Теперь концентрация справа, как это видно из «маленького» треугольника на рис. 4.2:
Ведь tg α — это производная. Точно также найдем, что слева
Рис. 4.2. К объяснению закона диффузии n + = n 0 + Δ n = n 0+ l tgα концентрации числа частиц или их массы Число частиц есть произведение концентрации n +(или n –) на тот объем, из которого молекулы успевают долететь до выделенного сечения за время Δ t. Расстояние, с которого долетят до этого сечения молекулы (они движутся в среднем со скоростью á V ñ), будет á V ñΔ t. Объем, соответственно, будет Δ V = á V ñ S Δ t. Необходимо учесть также, что в силу хаотичности движения все направления в пространстве равноправны, и вдоль выделенного для удобства направления x «эффективно» летит 1/6 часть всех молекул. Этот вопрос подробно обсуждался при выводе основного уравнения молекулярно-кинетической теории (см. гл. 1). Напомним, что 1/3 следует из того, что любую скорость можно разложить в пространстве на 3 проекции на оси, и еще возможны два направления — по оси и против нее. Итак:
И тогда поток в соответствии с формулой (6.5) будет
Из этой формулы, прежде всего, видно, что поток частиц в направлении какой-либо оси пропорционален производной от числа частиц (концентрация n просто пропорциональна числу частиц N = n Δ V) по переменной, откладываемой вдоль той оси, по которой направлен поток. Так формулируется закон Фика — закон диффузии. Если бы требовалось найти поток вдоль оси у, нужно лишь производную d / dx заменить производной по этой новой оси — d / dy. Величина, проекция которой определяется производными по осям координат, называется градиентом:
Это математическая запись закона диффузии — закона Фика. Во все соотношения, приведенные ранее в этой главе, входила проекция потока на ось, соответствующую переменной, по которой бралась производная. Величина
называется коэффициентом диффузии и определяется параметрами газа. Размерность коэффициента диффузии очевидна — квадратный метр за секунду (м2/с). Диффузия возможна не только в газе, но и в жидкостях и твердых телах (при тесном их соприкосновении). И в жидкостях, и в твердых телах молекулы одного сорта самопроизвольно проникают из областей, где их концентрация высока, в те области, где их концентрация низкая. Оказывается, что и в этом случае — случае жидкостей или твердых тел — закон диффузии можно записать в том же виде:
Но, конечно, величина коэффициента диффузии уже не равна á V ñ l /3, как для газа, а зависит только фактически от молекулярного устройства конкретного вещества и мало меняется даже при изменении температуры (конечно при небольших ее изменениях и вдали от фазовых переходов «твердое тело — жидкость» и «жидкость–пар»). Главное свойство сохраняется: поток диффузии пропорционален градиенту концентрации (или градиенту плотности ρ, ведь плотность прямо пропорциональна концентрации). Тогда закон Фика для массывещества можно сформулировать так: масса вещества, переносимая за единицу времени через единицу площади в направлении, перпендикулярном этой площади, прямо пропорциональна изменению (градиенту) плотности в этом направлении. Первоначально этот закон был открыт экспериментально. Для жидкостей и твердых тел коэффициенты диффузии собраны в справочниках. Для газов в справочниках приводятся коэффициенты диффузии при нормальных условиях (давлении р 0= 1 атм. и температуре Т 0= 273 К). К другим условиям коэффициент диффузии приводится с помощью известных зависимостей Итак, закон Фикав различных модификациях можно записать как
|

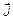 , изменением переносимой величины при проходе через единицу площади S за единицу времени Δ t. В случае диффузии диффузионный поток
, изменением переносимой величины при проходе через единицу площади S за единицу времени Δ t. В случае диффузии диффузионный поток 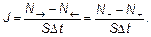 (4.4)
(4.4) , которая, напомню, определяется температурой газа (см., например, (5.1)):
, которая, напомню, определяется температурой газа (см., например, (5.1)):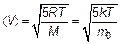 (4.5)
(4.5)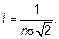 (4.6)
(4.6)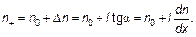 (4.7)
(4.7)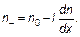 (4.8)
(4.8)
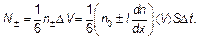 (4.9)
(4.9)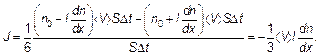 (4.10)
(4.10)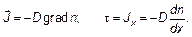 (4.11)
(4.11) (4.12)
(4.12)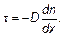 (4.13)
(4.13) и l ~ Т / р.
и l ~ Т / р.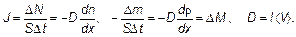 (4.14)
(4.14)


