Длина свободного пробега молекулы
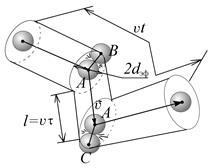
Молекулы в процессе теплового (хаотического) движения соударяются не только со стенкой, но и между собой. Длина пути, который молекула проходит между двумя последовательными столкновениями, называется длиной свободного пробега (рис. 4.1). Конечно, свободный пробегодной молекулы все время меняется, однако для большого числа молекул можно, как обычно, говорить о средней длине пробега.
Рис. 4.1. Длина свободного пробега молекулы Для вывода формулы рассмотрим молекулу А, движущуюся после столкновения с молекулой В прямолинейно со скоростью V до нового столкновения с молекулой С. Среднее число столкновений молекулы А за время t равно числу Z столк. Очевидно, что Z столкравно числу молекул, которые находятся в объеме цилиндра с основанием — кругом радиуса 2 d эфф, где величина d эфф — эффективный диаметр молекулы, такое расстояние, на котором одна молекула «достает» другую при столкновении. Можно сказать и по-другому: эффективный диаметр молекул — это диаметр такого шара, что эффект (отсюда «эффективный») от столкновения с этим шаром другой молекулы будет таким же, как и при столкновении реальных «рогатых» молекул. Оба эти определения приводят к примерно одинаковым числовым значениям диаметров, и поэтому эти определения можно в первом приближении считать эквивалентными. Эффективный диаметр различных молекул собран в таблицах справочников. Длина (высота) цилиндра, в котором находятся молекулы, сталкивающиеся с молекулой А, очевидно равна Vt. Тогда объем этого «столкновительного» цилиндра — p(2 d эфф)2 Vt /4 (площадь основания на высоту). При концентрации молекул n = N / V в таком объеме находится
Длина свободного пробегаl = V τ — путь (средний) между двумя столкновениями. Соответственно, τ — время, за которое молекула проходит длину свободного пробега, время между столкновениями. Таким образом, l — это весь путь Vt, деленный на число молекул (и, следовательно, столкновений) на этом пути Z столк, т. е.
где σ — площадь эффективного сечения (площадь круга) молекулы. Очевидно, что длина пробега не зависит ни от времени (что можно было ожидать), ни от скорости молекулы, что предвидеть было труднее. Конечно, зная ответ, можно понять, что при большей скорости молекула пролетает эту длину быстрее, а сам путь определяется только концентрацией — количеством «препятствий». Но до получения ответа такой вывод не напрашивался. При выводе формулы для l считалось, что движется только молекула А, а другие («препятствия») покоятся. Если учесть их движение, то появится числовой коэффициент. Длина свободного пробега станет:
Впрочем, часто этот коэффициент включают в площадь эффективного сечения.
|

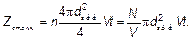 (4.1)
(4.1)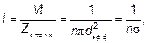 (4.2)
(4.2) (4.3)
(4.3)


