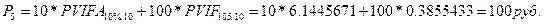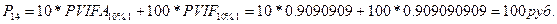Тема 6. 1. Вычисления по ценным бумагам
К основным ценным бумагам относятся облигации и акции. Облигация — это инструмент займа. Владелец облигации — кредитор, должник — эмитент облигации. Свойства облигации: 1. Облигация не дает права на участие в управлении имуществом 2. Облигация — частная ценная бумага. 3. Облигация обещает платежи по купонам, а затем погашение по
Для того чтобы оценить облигацию, необходимо найти ее современную стоимость. Введем обозначения: п — срок погашения облигации; N — ее номинал; q — купонная ставка (это процент от номинала).
Пример 1: на облигации указана купонная ставка в 10% годовых. Номинал облигации — 100 руб. Платежи по купонам производятся один раз в год. Это значит, что облигация принесет прибыль 10 руб. Если ежегодно получаемые по облигациям выплаты будут помещены на банковский депозит или инвестированы каким-либо иным образом и станут приносить ежегодный процентный доход I = Nq, то стоимость облигации Р будет равна сумме двух слагаемых — современной стоимости ее аннуитетов (серии ежегодных выплат процентных платежей) и современной стоимости ее номинала:
где PVIFA –(…Р.Value of Interest Faktor of Annuity)- коэффициент приведения аннуитета. [(1+i)n -1] / i. Его значения табулированы. PVIF = 1/ (1+i)n –коэффициент дисконтирования. Его значения табулированы
Решение. Оценим облигацию в момент выпуска
Рыночная цена облигации через год после выпуска:
Через 5 лет:
Через 14 лет:
Вывод: если купонная ставка равна среднерыночной (в данном случае ставке банка), то оценка облигации не меняется в течение всей жизни. Рыночная цена облигации в этом случае равна номиналу.
Возьмем среднерыночную ставку i =15%. Тогда рыночная цена облигации будет ниже номинала. В этом случае говорят, что облигация продается с дисконтом. Оценим облигацию в начале жизни, за 5 и за 14 лет до погашения и найдем величину дисконта: цена облигации в начале жизни – Ро = 70,76 руб., величина дисконта- 29,24 руб., цена облигации за 5 лет до погашения- Р5 =74,91 руб., величина дисконта - 25,09 руб., цена облигации за 14 лет до погашения- Р14 =95,65 руб., величина дисконта -4,35 руб. Возьмем среднерыночную ставку i =8%. Тогда рыночная цена облигации будет выше номинала, она будет продаваться с премией. Оценим облигацию в начале жизни. За 5 и 14 лет до погашения и найдем величину премии: цена облигации в начале жизни -117, 12 руб., величина премии -17, 12 руб., цена облигации до погашения – Р5 =113,42 руб., величина премии —13,42 руб., цена облигации за 14 лет до погашения — Р14 =101,85 руб., величина премии —1,85 руб.
Выводы: 1. Если рыночная ставка равна купонной ставке (q =i), то в течение всей жизни облигация оценивается по номиналу 2, Если рыночная ставка больше купонной ставки (i> q), то облигация оценивается ниже номинала. Облигация будет продаваться с дисконтом. С приближением даты выкупа происходит погашение дисконта. 3. Если рыночная ставка меньше купонной (i < q), то облигация оценивается выше номинала. Облигация будет продаваться с премией. Приприближении даты выкупа стоимость облигации понижается. Обусловлено это тем, что по ней уже выплачена большая часть доходов, и к моменту выкупа остается получить только ее номинальную стоимость.
|



 Пример 2. По облигации номинальной стоимостью 100 руб. в течение 15 лет (срок до ее погашения) будут выплачиваться ежегодно, в конце года — процентные платежи в сумме 10 руб. (q = 10%), которые могут быть помещены в банк под 10% годовых. Оценить облигацию в момент выпуска, через год после выпуска и за год до погашения облигации.
Пример 2. По облигации номинальной стоимостью 100 руб. в течение 15 лет (срок до ее погашения) будут выплачиваться ежегодно, в конце года — процентные платежи в сумме 10 руб. (q = 10%), которые могут быть помещены в банк под 10% годовых. Оценить облигацию в момент выпуска, через год после выпуска и за год до погашения облигации.

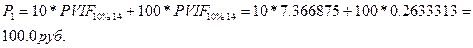
 .
.