Основные элементы сетевой модели
Основой СПУ является сетевая модель. Сетевая модель - это графическое изображение технологической последовательности и связи событий, каждое из которых выражает результат и показывает момент окончания входящих в него одной или нескольких работ. Основными элементами сетевой модели являются работа и событие. Работой называется процесс, приводящий к получению определенного результата, т. е. свершению события. Термин «работа» используется в СПУ в широком смысле слова и имеет три значения:
• фиктивная работа или зависимость - условный элемент, который вводится для отражения взаимосвязи между событиями. Фиктивная работа не требует ни затрат времени, ни ресурсов, но указывает, что возможность начала одной работы непосредственно зависит от окончания другой. На графике изображается пунктирной стрелкой (-->). Каждая работа в сетевом графике кодируется цифрами соединяющих событий (ij). Например, работа ij находится между i -м (предшествующим) событием и j-м (последующим) событием. Стрелки, изображающие работу на сетевом графике, с точки зрения длины и направления не имеют принятого для вектора смысла. Ихдлину, угол наклона вычерчивают произвольно. Направление стрелок определяет лишь связь между событиями по времени. Событие - это результат выполнения одной работы или нескольких, который может являться началом другой работы или нескольких работ. Событие фиксирует только факт окончания или начала одной или нескольких работ и не связано с затратами времени и ресурсов. Графически событие изображается в виде кружка или другой геометрической фигуры. Понятие «событие» может иметь следующие значения: • исходное событие - начало выполнения проекта (исходное событие не имеет предшествующих работ, в сети в него не входит ни одна работа); • завершающее событие - достижение конечной цели проекта (завершающее событие не имеет следующих за ним работ, поэтому в сети из него не выходит ни одной работы); • промежуточное событие, или просто событие, - результат одной или нескольких работ, дающий возможность начать одну или несколько следующих за ним работ. На рис. 4.6.2 в качестве примера изображена простейшая сетевая модель. События в ней обозначены кружками с указанием в верхних сегментах последовательного номера, а работы обозначены стрелками.
Рис. 1. Пример изображения сетевого графика (продолжительность работ принята в условных единицах времени) Продолжительность работы в сети может определяться по нормативам. В этом случае сеть называется детерминированной. Продолжительность работы определяется по формуле t(ij)= где t(ij) - продолжительность работы, дн.; Т - трудоемкость (ij) работы, ч; Ч i - количество исполнителей по данной работе, чел.; Тсм - продолжительность одной смены, ч. При отсутствии необходимых нормативов используется ожидаемая продолжительность работ -временная оценка, полученная на основе трех вероятностных оценок — минимальной, или оптимистической (tmin)> максимальной, или пессимистической (tmax), наиболее вероятной (tн.в)- Минимальная, или оптимистическая, оценка (tmin) - минимально необходимое время для выполнения работы при наиболее благоприятном стечении обстоятельств. Максимальная, или пессимистическая, оценка (tmax) - максимальное время, необходимое для выполнения работы при наиболее неблагоприятном стечении обстоятельств. Наиболее вероятная оценка (tн.в) - время выполнения работы при нормальных (чаще всего встречающихся) условиях выполнения данной или подобной работы. Все три вероятностные оценки времени указываются ответственными исполнителями данной работы. Сами по себе эти величины не могут служить характеристикой продолжительности работ, они являются исходными данными для расчета ожидаемого времени выполнения работы (tож). Величина tож представляет собой математическое ожидание или среднее статистическое значение трех оценок продолжительности работ, рассчитывается по одной из двух формул:
tож=
Найденные значения tож округляются до целых чисел. Вторая формула расчета tож чаще всего используется в тех случаях, когда затруднительно дать наиболее вероятную оценку продолжительности выполнения работ. Сетевая модель с вероятностными оценками называется в е р о я т н о с т н о й. Величиной неопределенности временных оценок вероятностных работ (
Работы с большими величинами дисперсии имеют высокую степень неопределенности, т. е. больший риск исполнения рассчитанных сроков работ, а работы с небольшими величинами дисперсии - высокую степень вероятности выполнения в ожидаемый срок. Возможны также сети со смешанными оценками продолжительности работ, т. е. когда часть работ имеет детерминированную оценку, а вторая часть - вероятностную оценку. Продолжительность работ может указываться на сетевом графике в виде цифр над стрелками (см. рис. 1).
|

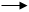 • действительная работа - процесс, требующий затрат времени и ресурсов, на сетевом графике изображается сплошной стрелкой ()
• действительная работа - процесс, требующий затрат времени и ресурсов, на сетевом графике изображается сплошной стрелкой () • ожидание - процесс, требующий затрат времени, но не требующий затрат ресурсов. На графике изображается штрихпунктирной стрелкой ()
• ожидание - процесс, требующий затрат времени, но не требующий затрат ресурсов. На графике изображается штрихпунктирной стрелкой ()
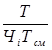 ,
, или tож=
или tож= 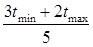 .
.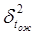 ) является дисперсия, которая определяется по формуле
) является дисперсия, которая определяется по формуле , или
, или  .
.


